Спосіб автоматичного керування об’єктом

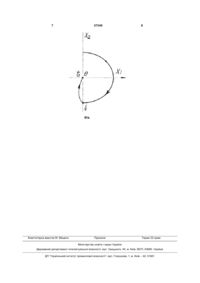
Спосіб автоматичного керування об'єктом, за яким формують сигнал керувальної дії, пропорційний сумі абсолютних значень сигналів розгалу 3 X10  0 ; X2 0  dX10 . dt 57349 (1) При цьому лінійна комбінація величини розгалуження Х1(0) і швидкості Х2(0) розгалуження дорівнює нульовому значенню а1·X1(0)+а2·Х2(0)=0, X1(0)=Х2(0)=0, (2) де а1, а2 - постійні коефіцієнти. При виконанні умови (2) запам'ятовується нульове розгалуження Х1(0)=0, а сигнал керувальної дії дорівнює також нульовому значенню. В деякий момент tn часу, що прийнятий за початковий, формується початкове розгалуження Х1n=Х1(tn)≠0, Х2n=Х2(tn)≠0, де X2n  dXn tn  . dt Припустимо також, що Х1n>0, Х2n>0 і на фазовій площині Х2=f(X1) початкове положення системи фіксують в першому квадранті. Лінійна комбінація Х1n, Х2n в момент tn часу приймає ненульове значення a1·X1n+a2·X2n≠0, (3) тому запам'ятовування сигналу керувальної дії не відбувається, а переміщення об'єкта має місце тільки під впливом початкових умов Х1n, Х2n. Величина сигналу керувальної дії дорівнює нульовому значенню. Таке переміщення об'єкта відбувається до моменту t1 часу, в який розгалуження приймає нульове значення, а швидкість розгалуження має ненульове значення a1·X11+a2·X2l=a10+а2Х21≠0, де (4) Х11=Х1(t1), Х21=Х2(t1). При умові (4) формується сигнал керувальної дії, що дорівнює величині (|Х11|+|Х21|)=|Х21| (5). Проведемо теоретичний аналіз запропонованого способу автоматичного керування об'єктом. Розглянемо математичну модель системи автоматичного керування у вигляді неоднорідного диференціального рівняння другого порядку d2X dX A 2 B  CX  f t  , dt dt (6) де А - інерційний коефіцієнт; В - коефіцієнт опору; С - коефіцієнт жорсткості; f(t) - сигнал зовнішньої дії. Однорідне диференціальне рівняння, що відповідає (6), має вигляд A d2X dX B  CX  0 . 2 dt dt (7) Рішення диференціального рівняння (7) визначають у вигляді X=Xaexp(St), де Ха - амплітудне значення; S - корінь характеристичного рівняння. Характеристичне рівняння для визначення двох коренів S1, S2 має вигляд AS2+BS+C=0. (8) Корені S1, S2 квадратного рівняння (8) мають вигляд S1   B  B  4AC ; 2A 2  B  B2  4AC S2  . 2A (9) 4 При умові, якщо B2  4AC  0 , корені S1, S2 характеристичного рівняння дійсні, різні і від'ємні. При цьому рішення диференціального рівняння (7) має вигляд: x(t)=С1ехр(S1t)+С2exp(S2t), (10) де C1, C2 - постійні коефіцієнти. Значення коефіцієнтів С1, С2 визначаються початковими умовами  X10  C10 expS1  0  C0 expS2  0  2   C10  C0 2 , (11) dX 0   X2 0  X10  1  C10S1 expS1  0  . dt   C0S2 expS2  0  C10S1  C0S2 2 2 (12) При заданні X1(0), X2(0) на підставі (11), (12)  отримаємо значення C10 , C0 із системи рівнянь 2  C10  C0  X10 2   0  S C0  X 0 S1C1 2 2 2   (13) а саме:  1 1  S2  S1 ; S1 S2 1  2  X10 1  S2X10  X2 0 X2 0 S2 (14) 1 X10  X2 0  S1X10 S1 X2 0 1 S2X10  X2 0 ;   S2  S1 X 0  S1X10 . (15) C0  2 2 S2  S1  C10  Рівняння (10) при урахуванні (15) приймає вигляд S X 0  X2 0 X 0  S1X10 xt   2 1 expS1t   2 expS2t  . S2  S1 S2  S1 (16) Розгалуження X(t) переміщення продовжується до моменту t1, часу, в який величина розгалуження X(t) дорівнює нульовому значенню, а величина швидкості dX розгалуження не дорівнює dt нульовому значенню S2 X10  X2 0 expS1t1   S2  S1 ; X 0  S1X10  2 expS2 t1   0 S2  S1 X11  X1t1   dX1t1 S1S2 X10  X2 0  expS1t1  dt S2  S1 . S X 0  S1X10  2 2 expS2t1 S2  S1 (17) X21  (18) Подальше переміщення системи по фазовій траєкторії на фазовій площині від точки Х11=0, Х12≠0 до точки Х11=0, Х22=0 відбувається під дією сили, яка дорівнює величині 5 57349 U12=(|Х11|+|X21|)=|X21|, (19) де Х21 визначається співвідношенням (18) S1S2X10  X2 0 expS1t1  S2  S1 , S X 0  S1X10  2 2 expS2t1 S2  S1 X21  (20) а X11=0 визначається співвідношенням (17). Тепер розгалуження переміщення (траєкторія руху) відповідає диференціальному рівнянню A d2X dX B  Cx  X21 , dt dt (21) рішення якого має вигляд  xt   C12 expS1t   C2 expS2t   2 X21 , C dx   S1C12 expS1t   S2C2 expS2t  2 dt (22) (23) при початкових умовах Xt1  X11  0 ; dXt1  X21  0 . dt (24)  Визначаємо коефіцієнти C12 , C2 при засто2 суванні (22), (23), (24) при t=t1,  X21  0, C  (25)  2 expS t   S C2 expS t ; X21  S1C1 11 2 2 21   X11  C12 expS1t1  C2 expS2t1  2  expS1t1 expS2t1  S2  S1expS1  S2 t1 ; S1 expS1t1 S2 expS2t1 (26) 1  X21 C  X21  expS2t1 S2 expS2t1 S    X21 expS2t1 2  1 ; C   (27) 2  expS1t1 S1 expS1t1 X21  S1  C   X21 expS1t11  ;  C  X21  (28)  C2  1  1  S  S   X21 expS2t1 2  1  X21  2  1 C  C  ; S2  S1expS1  S2 t1 S2  S1expS1t1 (29)  C2  2  2   S   S   X21 expS1t11 1   X21 1 1   C   C ; S2  S1expS1  S2 t1 S2  S1expS2t1 (30) Розгалуження переміщення X(t) продовжується до моменту t2 часу, для якого Х12=0, Х22=0. Таким чином, як відмічено у дослідженні [Емельянов С.В. Системы автоматического управления с переменной структурой. М.: Наука, с. 64], час наявності перехідного процесу для фазової траєкторії запропонованого способу автоматичного ке 6 рування об'єктами буде зменшений при порівнянні з відомим способом за рахунок більш високої швидкості розгалуження, а формування сигналу керувальної дії однієї полярності без її зміни приводить до спрощення технологічного режиму керування об'єктом. Спосіб автоматичного керування об'єктом реалізують на підставі наступного алгоритму. 1. Формують режим вільного переміщення досліджувальної системи під дією початкового значення величини розгалуження і швидкості розгалуження. 2. Фіксують і запам'ятовують в деякий момент часу величину сигналу швидкості при нульовому значенні сигналу розгалуження; в цей же момент часу формують сигнал керувальної дії, причому полярність сигналу керувальної дії протилежна полярності сигналу швидкості розгалуження. 3. Сигнал керувальної дії формують рівним по модулю значенню швидкості розгалуження при нульовому значенню розгалуження. Новим в технологічному режимі реалізації способу автоматичного керування об'єктом є проведення операції формування сигналу керувальної дії тільки на одній ділянці при виборі полярності цього сигналу протилежним полярності сигналу швидкості розгалуження при нульовому значенні розгалуження . Спосіб автоматичного керування об'єктом реалізують таким чином. 1. Установлюють випробуваний об'єкт на рухому платформу вібростенда електродинамічного типа при жорсткому з'єднанні з платформою (в вихідному стані платформа вібростенда урівноважена). 2. Формують на вібростенді сигнал керувальної дії за рахунок надходження скачка постійного струму в обмотку рухомої котушки збудження вібростенда. 3. Реєструють і запам'ятовують величину сигналу розгалуження і швидкість розгалуження за допомогою датчиків, установлених на об'єкті. 4. При нульовому значенню сигналу розгалуження фіксують і запам'ятовують значення сигналу швидкості розгалуження. 5. Формують сигнал керувальної дії в момент часу, в який величина сигналу розгалуження дорівнює нульовому значенню; полярність сигналу керувальної дії протилежна полярності сигналу швидкості розгалуження. 6. В момент часу при нульовому значенні сигналу розгалуження і сигналу швидкості розгалуження величину сигналу керувальної дії установлюють по значенню, яке дорівнює нулю. Таким чином, при використанні даної корисної моделі не виникає необхідність у формуванні сигналу керувальної дії при переході від одної ділянки до іншої при зміні полярності, що значно спрощує цілому технологічний процес способу автоматичного керування об'єктом. 7 Комп’ютерна верстка М. Мацело 57349 8 Підписне Тираж 23 прим. Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601