Спосіб автоматичного керування на основі зворотного зв’язку по відхиленню величини та фазового запізнення вихідного сигналу об’єкта керування

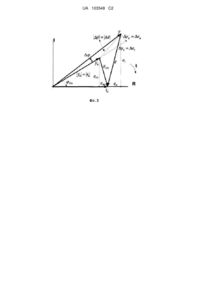
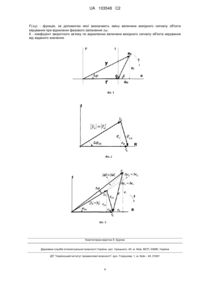
Реферат: Спосіб автоматичного керування (САК) на основі зворотного зв'язку по відхиленню величини та фазового запізнення вихідного сигналу об'єкта керування, належить до галузі автоматичного керування об'єктами, в тому числі нелінійними, довільного порядку, при наявності нестаціонарних затримок та недостатній інформації для побудови точної математичної моделі об'єкта. Ідея запропонованого САК заснована на визначенні вихідного сигналу регулятора на основі обчислення різниці між заданим значення вихідного сигналу об'єкта регулювання (уставкою) та вихідним сигналом об'єкта керування з врахуванням відхилення фазового запізнення, що виникає при порушенні усталеного режиму роботи. Для визначення відхилення фазового запізнення між довільними сигналами уставки та вихідним сигналом об'єкта керування використовується перетворення Гілберта, яке дозволяє представити їх у вигляді аналітичних сигналів. Використання такого способу керування дозволяє враховувати зміну стану інерційних елементів, які входять до складу об'єкта керування та досягати якісних характеристик САК при недостатній інформації для побудови точної математичної моделі об'єкта. UA 103548 C2 (12) UA 103548 C2 UA 103548 C2 5 Запропонована система автоматичного керування на основі зворотного зв'язку по відхиленню величини та фазового запізнення вихідного сигналу об'єкта керування належить до галузі техніки автоматичного керування (САК) об'єктами, в тому числі нелінійними, довільного порядку, при наявності затримок та недостатній інформації для побудови точної математичної моделі об'єкта. Рівень техніки. Існуючі системи автоматичного керування для своєї роботи мають математичну модель об'єкта керування, на основі якої можливо досягти заданих характеристик та показників якості, які визначаються, як правило, цільовою функцією або функцією якості виду:  10 15 20 25 30 35 40    1T Gu, e   lim  u2  r  y 2 dt   min  t 0 T  0   , де u - вихідний сигнал регулятора, r - задане значення вихідного сигналу об'єкта керування (уставка), у - виміряний вихідний сигнал об'єкта керування, e=r-у - похибка керування. Запропоновані на сучасний час різноманітні системи автоматичного керування на основі нечіткої логіки, штучних нейронних мереж та інших методів, як свідчить практика, не знаходять широкого використання у галузях техніки, промисловості, та у більш ніж 90 % випадків [1] використовується пропорційно - інтегрально-диференційний (ПІД) регулятор або його різновиди П, ПІ, ПД. Аналогами винаходу є САК з ПІД регуляторами, які використовуються в більшості систем автоматичного регулювання в техніці та промисловості [1, 2, 3], а також запропонований в [4] спосіб автоматичного регулювання об'єктом на основі обчислення векторної похибки автоматичного регулювання. Суть винаходу. В основу винаходу поставлено задачу якісного автоматичного керування об'єктами, в тому числі нелінійними, довільного порядку, при наявності нестаціонарних затримок та недостатній інформації для побудови точної математичної моделі об'єкта. Для максимального використання інформації про характер процесів, що протікають в об'єкті автоматичного керування по його виміряному вихідного сигналу, пропонується крім визначення різниці (нев'язки) між заданим сигналом (уставкою) та виміряним виходом об'єкта керування, додатково враховувати відхилення фазового запізнення при порушенні усталеного режиму роботи, що відрізняється від загальновживаного визначення похибки для вибраного прототипу ПІД регулятора, і визначається не тільки по різниці величин уставки r і вихідного сигналу об'єкта керування у під впливом збурень, але також і впливом відхилення фазового запізнення Δυ вихідного сигналу об'єкта керування, як вказано в [5, 6]. Обґрунтуємо використання пропонованої похибки. Інерційність, фізичні принципи роботи об'єктів керування, а також обмежена швидкість розповсюдження сигналів, є причиною фазових запізнень, що спостерігаються між сигналами входу, змінними стану та вихідного сигналу САК. Для похибки, що залежить від фазового запізнення вихідного сигналу об'єкта керування, визначимо функцію похибки комплексного аргументу (ФПКА) як різницю між заданою уставкою r та виходом об'єкта керування у, що визначається на комплексній площині С, дійсна вісь R якої співпадає з r, а уявна вісь I зміщена на кут /2 в Декартовій системі координат, що дозволяє врахувати відхилення фазового запізнення при порушенні усталеного режиму роботи. ФПКА тоді знаходиться як, фігура 1: e  r  y  eR  je1  r y cos  jy sin , eR  r  y  cos  e  cos ; e1  y  sin  e  sin  , (1) 45 50    e  e  y  sin    arctg 1   arcsin 1 ,   arcsin  y r e   2  2   R   r  y  2  r  y  cos  . Відхилення фазового запізнення може бути обчислено за допомогою перетворення Гілберта [7], визначивши сигнали r та у як аналітичні: ~t   r t   yt   ~t  y r y r  y t   r t   arctg yt   r t   ~t   ~t  , (2) y r ~ ~ де r(t), y(t) - дійсні складові аналітичних сигналів (фізичні сигнали), r t  , yt  - уявні складові аналітичних сигналів, що знаходяться за допомогою перетворення Гілберта. В усталеному режимі між вхідним та вихідним сигналами існує постійне фазове запізнення υN0, яке визначається стаціонарним станом інерційних елементів, які входять до складу об'єкта 1 UA 103548 C2 керування. Даному фазовому запізненню відповідає нормальна функція похибки комплексного аргументу (НФПКА) eN0 , фігура 2. При порушенні усталеного режиму роботи, з врахуванням що 5 10 15 20 25 30 35 40 45 50 y0  r , маємо Δе=у -у=у -(уcos(Δυ))+jysin(Δυ))=r-(уcos(Δυ))+jysin(Δυ)), у=уcos(Δυ)+jysin(Δυ), 0 0 Δy=(y0-уcos(Δυ))+jysin(Δυ)=(r-(ycos(Δυ))+jysin(Δυ)), фігура 3. Тоді з використанням обчислень Віртінгера [8], керування визначене як антиградієнт зміни ФПКА при порушенні усталеного режиму роботи:   1 cos2N    y   Kr  Fy  u  kde  2k r   cosN   2 cosN      , (3) де К - коефіцієнт зворотного зв'язку по відхиленню величини вихідного сигналу об'єкта керування від заданого значення (уставки), N - коефіцієнт зворотного зв'язку по відхиленню фазового запізнення вихідного сигналу об'єкта керування при порушенні усталеного режиму, F(Δυ) - узагальнююча функція, визначаюча зміну величини вихідного сигналу об'єкта керування при відхиленні фазового запізнення при порушенні усталеного режиму. Використання запропонованої САК на основі зворотного зв'язку по відхиленням величини та фазового запізнення вихідного сигналу об'єкта керування дозволяє уникнути недоліків традиційного ПІД-регулювання: насичення вихідного сигналу регулятора під впливом інтегральної складової та перерегулювання під впливом диференційної складової, а також досягти кращого рішення при проектуванні САК в умовах значної невизначеності математичної моделі об'єкта керування. Для доказу того, що запропонована САК може бути використана для керування різноманітними об'єктами, в тому числі нелінійними, довільного порядку, при наявності фазового запізнення та недостатній інформації для побудови точної математичної моделі об'єкта, достатньо привести вираз комплексної похибки для випадку Δυ=0, тобто для об'єкта керування для якого не враховується відхилення фазового запізнення при порушенні усталеного режиму: e2  r 2  y 2  y 2  2  r  y  cos  r  y 2  r  r  y , eR  r  y  cos  r  y , (4) eI  y  sin  0 . Тобто в цьому випадку значення ФПКА відповідає значенню похибки, що використовується для вибраного прототипу - ПІД регулятора, з послідуючим знаходженням інтегральної та диференціальної складових. 4. Перелік фігур, креслень. Фігура 1 - геометрична інтерпретація функції похибки комплексного аргументу (ФПКА). На фігурі для усталеного режиму роботи об'єкта керування позначено: е0 - функція похибки комплексного аргументу (ФПКА); r - сигнал уставки, відносно якого визначається відхилення фазового запізнення Δυ вихідного сигналу об'єкта; у - вихідний сигнал об'єкта керування; Δυ - фазове запізнення між сигналами уставки та вихідного сигналу об'єкта керування; eR - дійсна складова ФПКА; eI - уявна складова ФПКА; δ - аргумент ФПКА у полярній системі координат. Фігура 2 - геометрична інтерпретація нормальної функції похибки комплексного аргументу (НФПКА). На фігурі позначено: eN0 - нормальна функція похибки комплексного аргументу (НФПКА); y0  r0 - сигнали уставки та вихідного сигналу об'єкта керування, рівні по модулю; ΔυN0 - нормальне фазове запізнення між сигналами уставки та вихідного сигналу об'єкта керування в усталеному режимі; eR - дійсна складова НФПКА; eI - уявна складова НФПКА. Фігура 3 - геометрична інтерпретація приросту ФПКА при порушенні усталеного режиму роботи об'єкта керування. На фігурі позначено: eN0 - нормальна функція похибки комплексного аргументу (НФПКА); y0  r0 - сигнали уставки та вихідного сигналу об'єкта керування, рівні по модулю; 2 UA 103548 C2 5 10 15 20 25 30 35 ΔυN0 - нормальне фазове запізнення між сигналами уставки та вихідного сигналу об'єкта керування в усталеному режимі; eR0 - дійсна складова НФПКА; еI0 - уявна складова НФПКА; у - сигнал комплексного вихідногосигналу об'єкта керування при порушенні усталеного режиму; y  e - прирости комплексного вихідного сигналу та ФПКА об'єкта керування при порушенні усталеного режиму роботи; Δυ - відхилення фазового запізнення при порушенні усталеного режиму роботи; Δys=Δes- прирости синфазних (дійсних) складових комплексного вихідного сигналу та ФПКА об'єкта керування при порушенні усталеного режиму роботи; Δyq=Δeq - прирости квадратурних (мнимих) складових комплексного вихідного сигналу та ФПКА об'єкта керування при порушенні усталеного режиму роботи. 5. Відомості, які підтверджують можливість здійснення винаходу. Здійснення запропонованої САК засновано на тому, що для вимірювання відхилення фазової затримки Δυ між довільною заданою уставкою r та виміряним довільним вихідним сигналом об'єкта керування у, при порушенні його усталеного режиму, можливо використати перетворення Гілберта [4-7] для їх представлення y вигляді аналітичних сигналів. Тоді відхилення фазової затримки може бути визначена через складові аналітичних сигналів як (2). Джерела інформації: 1. Li. Y., Ang К. Н. and Chong G. С. Y., Patents, software and hardware for PID control: an overview and analysis of the current art. IEEE CONTROL SYSTEMS MAGAZINE 26(1), 2006, pp. 4254. 2. Проектирование систем управления / Г.К. Гудвин, С.Ф. Гребе, М.Э. Сальгадо. - М.: БИНОМ. Лаборатория знаний, 2004.-911 с., ил. 3. Современные системы управления / Р. Дорф, Р. Бишоп. Пер. с англ. Б.И. Копылова - М.: Лаборатория Базовых Знаний, 2002.-832 с.: ил. 4. Агамалов О.Н. Патент України на винахід № 91398 Спосіб автоматичного регулювання об'єктом на основі обчислення векторної похибки автоматичного регулювання, бюлетень № 14. 5. Oleg Agamalov, Geometrical Model of Plant Presented on a State Surface of a Complex Error th (№ 650-655). 10 International Conference on Signal Processing, Robotics and Automation (ISPRA2011), Cambridge, UK, February 20-22, 2011. 6. Агамалов О. Н. Геометрическая модель системы управления, представленная на поверхности комплексной ошибки II Международный научно-технический журнал проблемы управления и информатики".-2011. - №3. - с. 25-41. 7. Poularikas A.D., The Transforms and Applications Handbook: Second Edition, CRC Press, 2000. 8. Kreutz-Delgado K. The complex gradient operator and the CR-calculus, in: Lecture Supplement ECE275A, 2006, pp. 1-74. 40 ФОРМУЛА ВИНАХОДУ 45 50 55 Спосіб автоматичного керування (САК) на основі зворотного зв'язку по відхиленню величини та фазового запізнення вихідного сигналу об'єкта керування, в якому зворотній зв'язок по відхиленню величини та фазового запізнення вихідного сигналу об'єкта керування використовують для формування сигналу керування об’єктом керування, в якому використовують різницю величин між заданим значенням r та вихідним значенням сигналу об'єкта керування у, який відрізняється тим, що додатково для формування сигналу керування, враховують відхилення фазового запізнення  між заданим значенням r та вихідним значенням сигналу об'єкту керування у, що виникає при порушенні усталеного режиму роботи об'єкта керування, та сигнал керування формують відповідно до виразу: u=K[r-yF()] ; де u - сигнал керування; r - значення (модуль) заданого вихідного сигналу об'єкта керування, відносно якого визначають відхилення величини та фазового запізнення вихідного сигналу об'єкта керування; y - значення (модуль) вихідного сигналу об'єкта керування;  - відхилення фазового запізнення між r та y, яке виникає при порушенні усталеного режиму роботи об'єкта керування, що визначається за допомогою перетворення Гілберта; 3 UA 103548 C2 F() - функція, за допомогою якої визначають зміну величини вихідного сигналу об'єкта керування при відхиленні фазового запізнення ; К - коефіцієнт зворотного зв’язку по відхиленню величини вихідного сигналу об'єкта керування від заданого значення. Комп’ютерна верстка Л. Бурлак Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 4