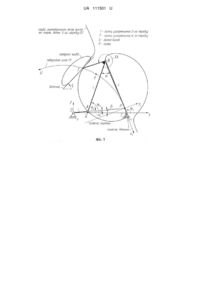
Шарнірний чотириланковий прямолінійно-напрямний механізм, побудований з використанням точки розпрямлення 5-го порядку
Формула / Реферат
Шарнірний чотириланковий механізм, що має основу, на якій встановлено кривошип, коромисло і шатун у вигляді двоплечого важеля, одне плече якого шарнірно зв'язано з кривошипом та коромислом, а інше плече виконано з можливістю опису його шатунною точкою кривої, яка на частковій ділянці траєкторії наближається до прямої лінії, причому за шатунну точку механізму приймається точка розпрямлення 5-го порядку, яка визначається як точка перетину поворотного кола з кривою геометричного місця точок, що характеризуються дотиком не нижче 5-го порядку зі своїми дотичними колами, за формулами:
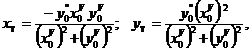
де ![]() - похідні відповідно 2-го та 5-го порядків від переміщення полюса миттєвого обертання шатунної площини.
- похідні відповідно 2-го та 5-го порядків від переміщення полюса миттєвого обертання шатунної площини.
Текст
Реферат: Шарнірний чотириланковий механізм має основу, на якій встановлено кривошип, коромисло і шатун у вигляді двоплечого важеля, одне плече якого шарнірно зв'язано з кривошипом та коромислом, а інше плече виконано з можливістю опису його шатунною точкою кривої, яка на частковій ділянці траєкторії наближається до прямої лінії, причому за шатунну точку механізму приймається точка розпрямлення 5-го порядку, яка визначається як точка перетину поворотного кола з кривою геометричного місця точок, що характеризуються дотиком не нижче 5-го порядку зі своїми дотичними колами, за формулами: x де ' V V y '0 x 0 y 0 x y ; y V 2 V 2 0 0 ' V V y '0 , x 0 , y 0 - похідні x y ' V y '0 x 0 2 V 2 0 V 2 0 , відповідно 2-го та 5-го порядків від переміщення полюса миттєвого обертання шатунної площини. UA 111501 U (54) ШАРНІРНИЙ ЧОТИРИЛАНКОВИЙ ПРЯМОЛІНІЙНО-НАПРЯМНИЙ МЕХАНІЗМ, ПОБУДОВАНИЙ З ВИКОРИСТАННЯМ ТОЧКИ РОЗПРЯМЛЕННЯ 5-ГО ПОРЯДКУ UA 111501 U UA 111501 U 5 10 15 20 25 30 35 40 45 50 Корисна модель належить до машинобудування, а саме до важільних плоских напрямних механізмів, шатунна точка яких наближено описує пряму лінію деякої довжини при неперервному обертовому русі вхідної ланки механізму (кривошипу). Синтез таких механізмів представляє собою одну з найскладніших задач у теорії механізмів та машин. Як відомо, існує два основних напрямки у синтезі таких механізмів: одним з напрямків є використання алгебраїчних методів Чебишева з використанням умов найкращого наближення функцій [1. - С. 675], які полягають у наявності максимально можливої кількості вузлів інтерполяції між заданою та замінювальною функціями з рівномірним характером зміни відхилень, що розглядається, зокрема, у [3,5]. Іншим напрямком у синтезі прямолінійно-напрямних механізмів є використання методів кінематичної геометрії, що полягають у використанні певних особливих точок шатунної площини, які дозволяють отримувати шатунні криві з ділянками наближено постійної кривизни таким чином можна отримувати шатунні криві з наближенням деякої ділянки до дуги кола або прямої лінії. Зокрема одним з можливих варіантів є шарнірний чотириланковий прямолінійнонапрямний механізм, побудований з використанням точки Болла [1. - С. 1068, рис. 864] (прототип), яка визначається в заданому положенні шатунної площини як точка перетину поворотного кола, що є геометричним місцем точок розпрямлення або перегинів шатунних кривих, з кривою кругових точок, що представляє собою геометричне місце точок, які забезпечують дотик не нижче 3-го порядку зі своїми дотичними колами. Таким чином, в деякому околі від точки Болла на шатунній кривій можна отримати ділянку, що наближається до прямої лінії. Сучасними науковими роботами, в яких розглядається проектування важільних прямолінійно-напрямних механізмів на базі точок Болла є, наприклад, монографія вчених Уанга Д. та Уанга У. [7. - С. 160], а також Уіна, Хана та ін. [6]. Як особливі точки шатунної площини можуть бути використані зокрема також точки розпрямлення 4-го порядку, що розглядались у роботі [4. - С. 71]. В основу корисної моделі поставлена задача - проектування шарнірного чотириланкового прямолінійно-напрямного механізму, який можна спроектувати з використанням інших шатунних точок механізму порівняно з прототипом. Поставлена задача вирішується таким чином, що як шатунні точки важільних механізмів приймаються інші особливі точки, що визначаються за допомогою методів кінематичної геометрії, а саме - точки розпрямлення 5-го порядку, що в загальному випадку визначаються як точки перетину поворотного кола (1), які є геометричним місцем розпрямлення або перегинів шатунних кривих, що описують дані точки, з кривою (2), що є геометричним місцем точок, які забезпечують дотик 5-го порядку зі своїми дотичними колами. Фіг. 1, 2 ілюструють запропоновану корисну модель. Фіг. 1. - Прямолінійно-напрямний шарнірний чотириланковий механізм з точкою розпрямлення 5-го порядку як шатунної. Фіг. 2. - Приклади шатунних кривих механізмів, синтезованих за точками розпрямлення 5-го порядку. Шарнірний чотириланковий механізм (фіг. 1) має основу 0, на якій встановлено кривошип 1, коромисло 3 і шатун 2 у вигляді двоплечого важеля, одне плече якого шарнірно зв'язано з кривошипом / та коромислом 3, а інше плече виконано з можливістю опису його шатунною точкою Т кривої, яка на частковій ділянці траєкторії наближається до прямої лінії, причому за шатунну точку механізму приймається точка розпрямлення 5-го порядку. Точки розпрямлення 5-го порядку визначаються в загальному випадку для будь-якого положення шатунної площини механізму. Якщо, відповідно до рекомендацій [1. - С. 1060], прийняти кутову швидкість обертання шатунної площини ω = 1, розмістити початок системи координат у Р полюсі миттєвого обертання шатунної площини та направити вісь абсцис вздовж полюсної дотичної, тоді рівняння поворотного кола в неявному вигляді запишеться наступним чином: 2 2 х +у -у"0у = 0, 55 (1) де у"0 - прискорення полюса Р миттєвого обертання шатунної площини механізму. Рівняння кривої (в неявному вигляді), що представляє собою геометричне місце точок, які забезпечують дотик 5-го порядку зі своїми дотичними колами має наступний вигляд: x 2 V V ' ' ' ' ' ' y 2 x 0 x y 0 y 5 yIV 2x '0' 2y '0 x x IV 2y '0' y 2y '0 y '0' x 2 y 2 y '0 y 0 , 0 0 1 (2) UA 111501 U 5 10 ' ' де y '0 , y '0' , x IV , yIV , x V , y V - прискорення та похідні вищих порядків від переміщення полюса Р 0 0 0 0 миттєвого обертання шатунної площини. Таким чином, якщо точка розпрямлення 5-го порядку, що визначається як точка перетину кривих (1) та (2), буде прийнята за шатунну точку механізму, в результаті вона буде описувати шатунну криву, що на деякій своїй ділянці в околі цієї точки буде наближатись до прямої лінії. Алгоритм проектування механізму наступний. 1. Задаємось довжиною кривошипа r=lOA, шатуна b=lAB, коромиcла с = lBC, а також кутом повороту кривошипа φ1, для якого в шатунній площині будемо визначати точку розпрямлення 5го порядку. За модуль довжини прийнято відстань між осями нерухомих шарнірів d=lOC=1. Визначаємо координати точки А механізму (кінця кривошипа) в системі координат хОу: XA=rcosφ1; YA=rsinφ1. (3) 2. Обчислюємо кути φ2 та φ3, що визначають положення відповідно шатуна b коромисла с механізму: 15 2 ; 3 . (4) де arctg / 1; . Для розрахунку шуканих кутів додатково визначаємо наступні величини: b 2 2 c 2 arccos 2b 2 2 2 , arccos b c 2bc ; 2 1 2 . (5) 20 3. Обчислюємо координати точки В механізму: XB=1+c cosφ3; YB=c sinφ3. 25 (6) 4. Обчислюємо координати полюса Р миттєвого обертання шатунної площини та миттєвого полюса Q відносного руху шатуна 2 та коромисла 3 механізму (в системі координат хОу): tg 3 ; tg 1 ; Q ; Q 0. tg 3 tg 1 (7) 5. Визначаємо прискорення полюса Р миттєвого обертання шатунної площини механізму: ' y '0 , sin 3 (8) 30 де кут нахилу осі колінеації arctg / Q , / cos 1 . 6. Визначаємо похідні 3-го порядку від переміщення полюса Р миттєвого обертання шатунної площини механізму (швидкість зміни прискорення полюса миттєвого обертання): ' x '0 k 1k 22 k 2k 12 k k k 1k 21 ' ' . 3y '0 , y '0' 2 11 k 11k 22 k 12k 21 k 11k 22 k 12 k 21 (9) 35 Коефіцієнти, що входять у (9) визначаються наступним чином: k 11 x x 2 y 2 ; k 12 y x 2 y 2 ; k 1 3y '' x y ; 0 k 21 x x 2 y 2 ; k 22 y x 2 y 2 ; k 2 3y '' x y ; 0 де координати шарнірів А та В в повернутій системі координат х1Ру1: 2 (10) UA 111501 U x cos t sin t , y cos t sin t , x cos t sin t , y cos t sin t . Кут нахилу полюсної дотичної: t 1 3 . 7. Визначаємо похідні 4-го порядку від переміщення полюса Р миттєвого обертання шатунної площини механізму: 5 x IV m4 m1 ; yIV m5 y '' m2 . 0 0 0 (11) Коефіцієнти m1…m5 визначаються наступним чином: 2 ' ' ' ' m1 4y '0' ; m2 4x '0' 6y '0 ; m3 3 y '0 m4 1 4x ''' y ''' 0 0 3y '' 0 4y ''' ; 0 ; (12) 3 x ''' 3y '' 4x ''' 6y '' 4 y ''' 0 0 0 0 0 m5 2 (13) , 3y '' 0 10 де коефіцієнти К1…К5, що входять у (13): x 1 4 x 5 y 2 y 2 3 x y / x 2 ; 2 y ''' 4x ''' 6y '' ; 4 m 3 x ''' ; 0 0 0 0 3 15 2 2 y (14) x2 y2 2 x2 x x x2 4 x2 y x2 y 5 ' ; 5 m 3 y '0' . x x y x y x (15) 8. Визначаємо похідні 5-го порядку від переміщення полюса Р миттєвого обертання шатунної площини: V x 0 1 ' 5y x 2 y 2 x 2 y 2 y '0 V y0 1 2y '' y ''' 0 0 x x y / y x 2 y y 2x 2y x x 2 y y ; x x y / y x y 5 y y x y y 2x 2y x x 2 y y x y y x y x2 y2 x2 y2 '' ''' IV ''' '' 2y 0 y 0 y 0 2x 0 2y 0 x ' ' ' 5 x 2 y 2 y '0 y 2y '0 y '0' y IV 0 IV 0 IV 0 ''' 0 ''' 0 ''' 0 2 '' 0 '' 0 2 IV 0 IV 0 ''' 0 ''' 0 (16) '' 0 2 2 0 2 2 IV x0 / y . (17) 9. Визначаємо точку розпрямлення 5-го порядку для заданого положення шатунної площини як точку перетину кривої (1) та кривої (2), у системі координат х1Ру1: 20 x 25 V V y '' x 0 y 0 0 V 2 x0 V 2 y0 ; y x y V y '' x 0 0 2 V 2 0 V 2 0 . (18) 10. Визначаємо координати точки розпрямлення 5-го порядку Т у базовій системі координат хОу. Для цього проведемо перетворення системи координат за наступними формулами: XΤ = XP – xΤcosαt+yΤsinαt; YΤ = YΡ - уΤ cosαt-xΤ sinαt (19) 11. Проектуємо важільний чотириланковий механізм, у якого довжина другого плеча шатуна k=lBT та кут Ω його злому визначає положення шатунної точки, як така буде прийнята знайдена точка розпрямлення 5-го порядку: k l 2 2 , (20) 3 UA 111501 U 180 2 arctg , 0 360 . (21) 12. Кут нахилу прямолінійної ділянки шатунної кривої визначається наступним чином: ' ' arctg y '0 cos t / y '0 sin t . 5 10 15 20 25 30 (22) Слід відзначити, що оскільки кут , а також всі інші кути, значення яких визначаються через функцію arctg(x), можуть змінюватись від 0 до 360°, для їх визначення слід скористатись не звичайною функцією арктангенса, а функцією arctan 2 y, x , де у, х - відповідно чисельник та знаменник у виразі (22). Ця функція є у більшості сучасних мов програмування. Як видно з прикладу, зображеного на фіг. 1, знайдена особлива точка - точка розпрямлення 5-го порядку, не збігається іншими відомими особливими точками, які використовуються для проектування важільних прямолінійно-напрямних механізмів та визначає нове сімейство таких механізмів. На фіг. 2 показано приклади шатунних кривих механізмів, синтезованих за допомогою точок розпрямлення 5-го порядку, які визначені для різних положень шатунної площини механізму (на фіг. вказано відповідні кути повороту кривошипа). Джерела інформації: 1. Артоболевский И.И. Синтез плоских механизмов. / И.И. Артоболевский, Н.И Левитский, С.А. Черкудинов. - М.: Физматгиз, 1959. - 1084 с. 2. Геронимус Я. Л. Геометрический аппарат теории синтеза плоских механизмов. - М.: Гос. издательство физ.-мат. литературы, 1962. - 400 с. 3. Киницкий Я.Т. Шарнирные механизмы Чебышева с выстоем выходного звена / Я. Т. Киницкий. - К.: Вища школа, 1990. - 232 с. 4. Харжевський В.О. Синтез важільних прямолінійно-напрямних механізмів та механізмів із зупинкою вихідної ланки на базі шарнірного чотирилан-кового механізму: дис… канд. техн. наук: 05.02.02 / В.О. Харжевський; Хмельницький держ. ун-т. - Хмельницький, 2004. - 262 с 5. Gassmann V. Synthese von Geradffihrungen mit ebenen Viergelenkgetrieben, Hamburg, Universitat der Bundeswehr Diss., 2000. - 102 p. 6. Yin L. Synthesis method based on solution regions for planar four-bar straight-line linkages / L.Yin, J.Han, C.Mao, J.Huang, T.Yang //Journal of Mechanical Science and Technology, 26 (10) 2012, С 3159-3167. 7. Wang D. Kinematic Differential Geometry and Saddle Synthesis of Linkages /Wang D.,Wang W.-John Wiley & Sons Singapore Pte. Ltd., 2015.-450 p. ФОРМУЛА КОРИСНОЇ МОДЕЛІ 35 40 Шарнірний чотириланковий механізм, що має основу, на якій встановлено кривошип, коромисло і шатун у вигляді двоплечого важеля, одне плече якого шарнірно зв'язано з кривошипом та коромислом, а інше плече виконано з можливістю опису його шатунною точкою кривої, яка на частковій ділянці траєкторії наближається до прямої лінії, причому за шатунну точку механізму приймається точка розпрямлення 5-го порядку, яка визначається як точка перетину поворотного кола з кривою геометричного місця точок, що характеризуються дотиком не нижче 5-го порядку зі своїми дотичними колами, за формулами: x 45 ' V V y '0 x 0 y 0 V 2 x0 V 2 y0 ; y x y ' V y '0 x 0 2 V 2 0 V 2 0 , ' V V де y '0 , x 0 , y 0 - похідні відповідно 2-го та 5-го порядків від переміщення полюса миттєвого обертання шатунної площини. 4 UA 111501 U Комп’ютерна верстка А. Крижанівський Державна служба інтелектуальної власності України, вул. Василя Липківського, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут інтелектуальної власності”, вул. Глазунова, 1, м. Київ – 42, 01601 5
ДивитисяДодаткова інформація
МПК / Мітки
МПК: F16H 21/00
Мітки: використанням, прямолінійно-напрямний, побудований, шарнірний, порядку, 5-го, чотириланковий, механізм, точки, розпрямлення
Код посилання
<a href="https://ua.patents.su/7-111501-sharnirnijj-chotirilankovijj-pryamolinijjno-napryamnijj-mekhanizm-pobudovanijj-z-vikoristannyam-tochki-rozpryamlennya-5-go-poryadku.html" target="_blank" rel="follow" title="База патентів України">Шарнірний чотириланковий прямолінійно-напрямний механізм, побудований з використанням точки розпрямлення 5-го порядку</a>
Попередній патент: Дросель регульований
Наступний патент: Запал машини безперервного лиття заготівок
Випадковий патент: Муфта запобіжна з складеною зіркоподібною пружиною