Спосіб підвищення швидкості навчання систем термінального керування в умовах завад

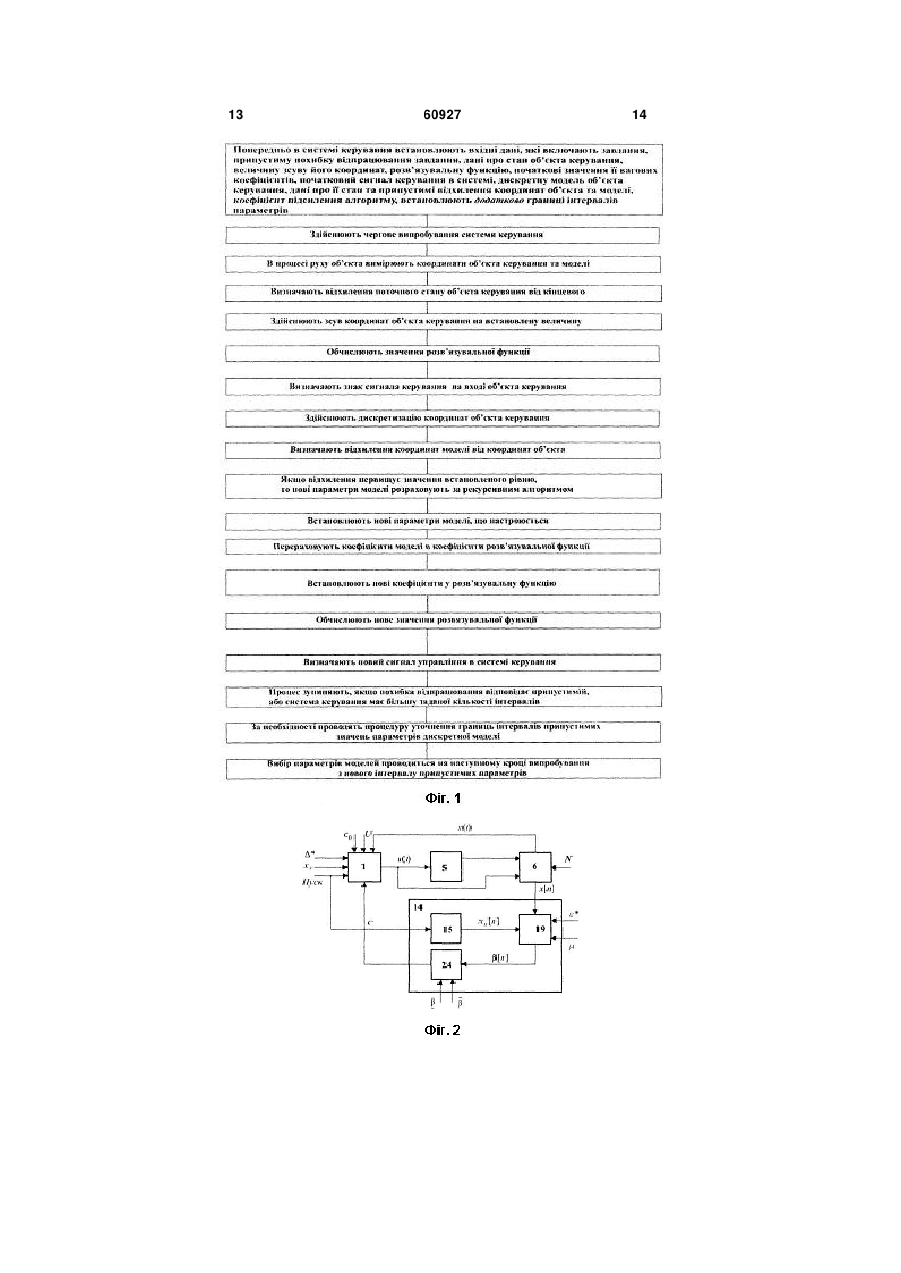
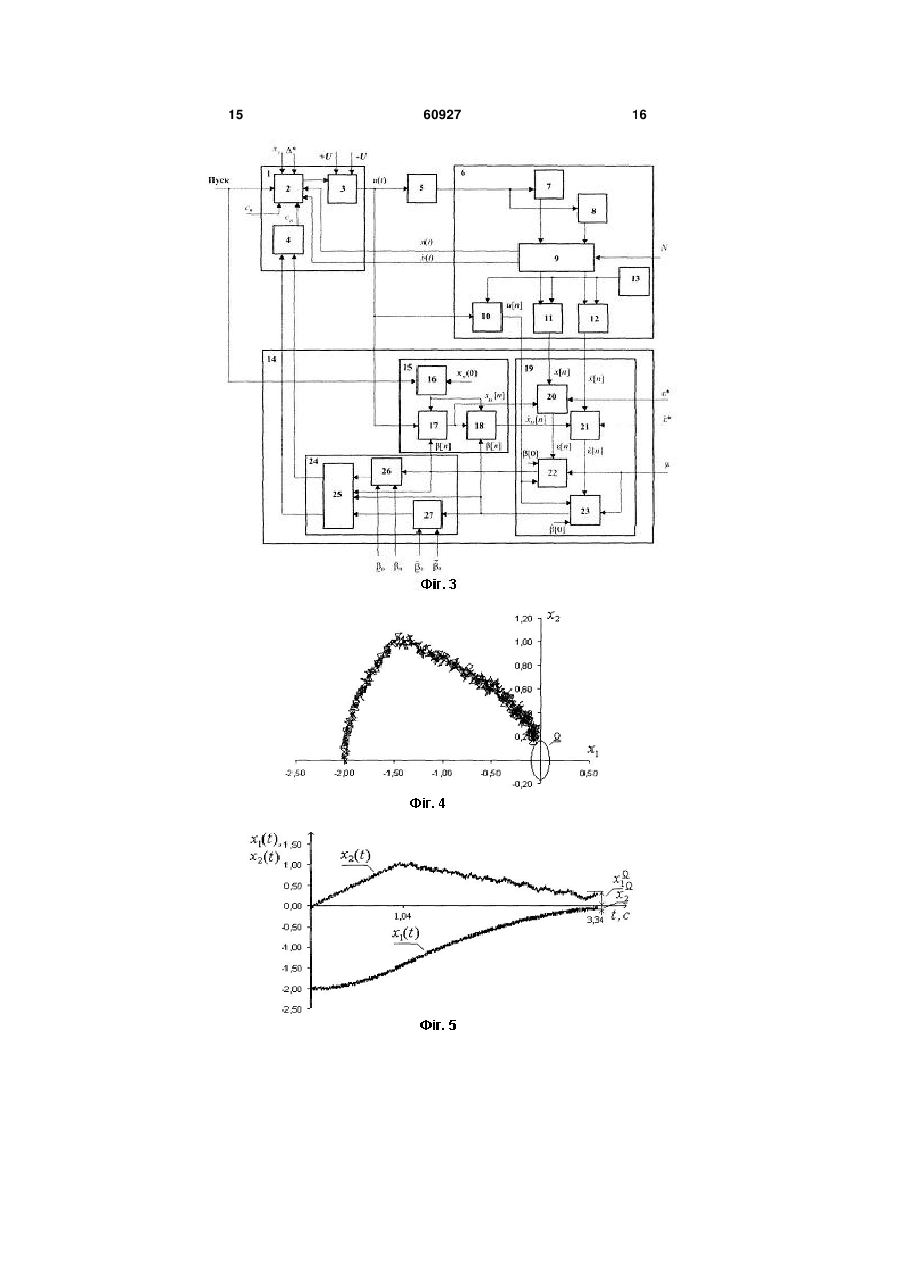
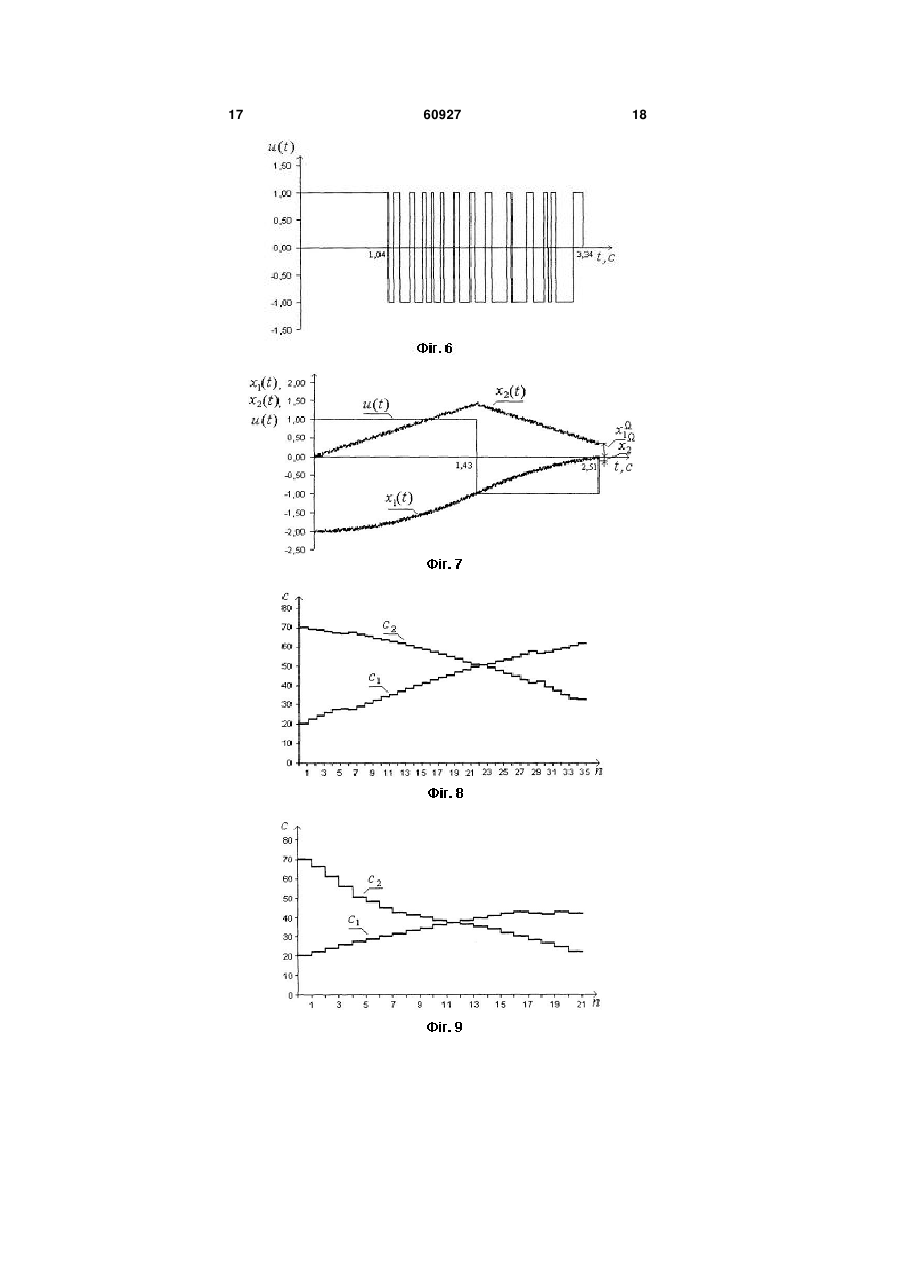
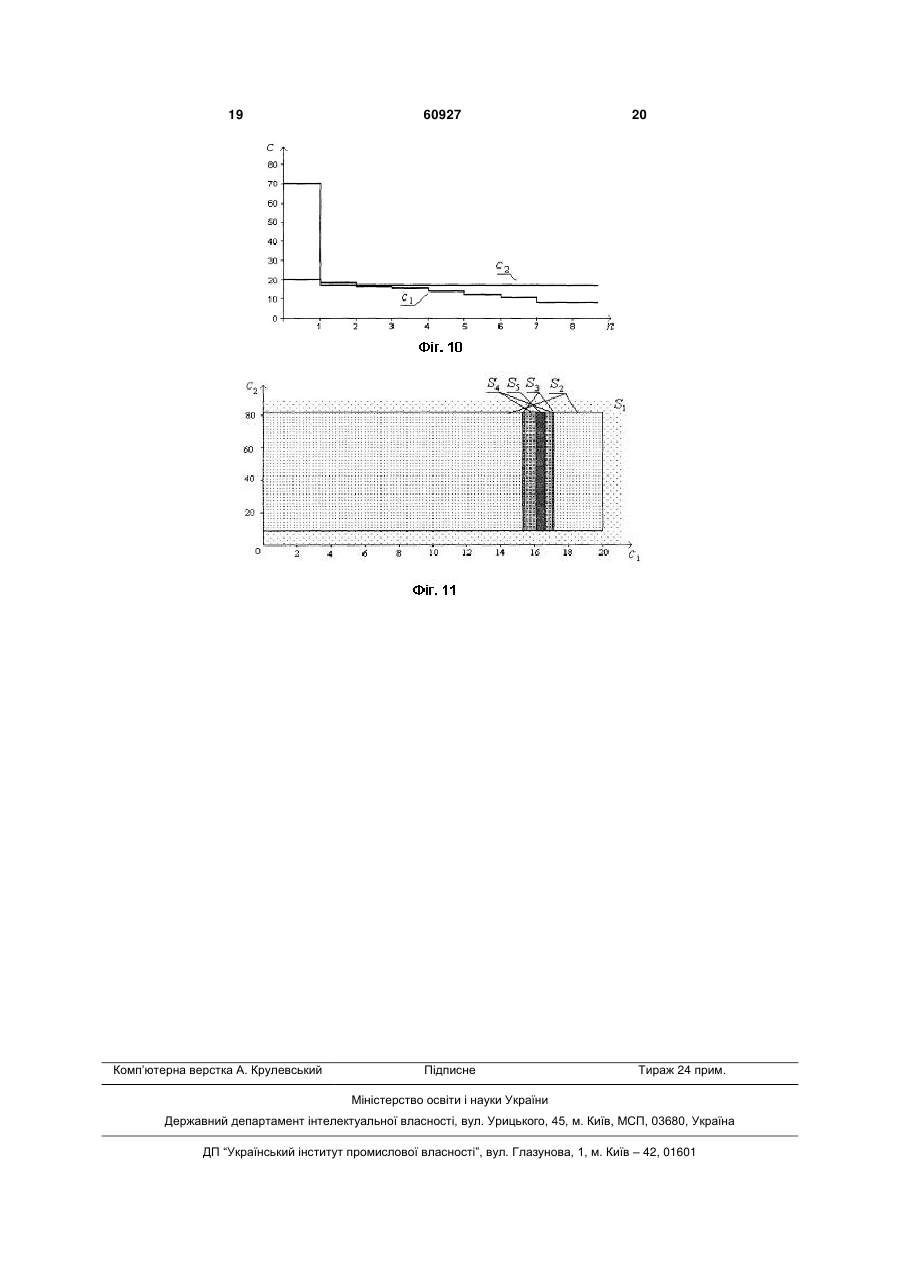
1. Спосіб підвищення швидкості навчання систем термінального керування в умовах завад, при якому в системі керування попередньо встановлюють вхідні дані, що включають завдання, припустиму похибку відпрацювання завдання об'єктом керування, дані про стан об'єкта керування, величину зсуву його координат, встановлюють також розв'язувальну функцію, початкові значення її вагових коефіцієнтів, початковий сигнал керування в системі, встановлюють також і дискретну модель об'єкта з початковим станом, рівним початковому стану об'єкта керування, порогові рівні відхилення координат об'єкта керування від моделі, встановлюють і коефіцієнт підсилення алгоритму дискретної корекції та в процесі руху вимірюють координати об'єкта керування, відхилення поточного стану об'єкта від кінцевого, в разі досягнення похибкою бажаного значення процес керування в системі завершують, в протилежному випадку здійснюють зсув координат об'єкта керування, за зсунутими координатами обчислюють нове значення розв'язувальної функції, за знаком якого визначають сигнал керування в системі, в процесі руху об'єкта також проводять дискретизацію координат об'єкта, визначають міру їх відхилення від координат мо U 2 UA 1 3 параметри об'єкта, що впливають на параметри системи керування, є невідомими або вони змінюються при русі. Рух динамічного об'єкта до кінцевого стану забезпечується системою термінального керування та здійснюється в умовах впливу завадових сигналів, які збільшують тривалість процесу керування та зменшують його точність. До структурного складу такої системи окрім інформаційної, керуючої частин та об'єкту керування відноситься і механізм адаптації (самонастроювання), який тим чи іншим чином підстроює параметри керуючого пристрою для забезпечення найменшого часу відпрацювання завдання. Механізм адаптації за використанням деякої інформації та поточного керування формує нові значення параметрів керуючого пристрою. Особливістю систем термінального керування є можливість застосування сигналів максимальної величини, знак яких за необхідністю змінюється на протилежний. Зміна знаку сигналу керування може бути здійснена за вимірами часу або за вимірами координат об'єкта керування, за якими обчислюється деяка функція, яку називають розв'язувальна, та знак її визначає знак поточного сигналу керування в системі. Останній тип побудови системи більш поширений тому, що при простішій технічній реалізації динамічна система має кращу точність за рівних умов. Інформаційна частина збирає дані про динаміку системи за показаннями датчиків, що характеризують стан об'єкта керування, та перетворює дані датчиків в сигнали зручного виду. Керуюча частина за допомогою пристроїв логіки та виконавчих елементів використовує сигнали з датчиків так, щоб досягти заданого термінального (кінцевого) стану. В умовах впливу зовнішнього середовища рух об'єкта керування відрізняється від оптимального (найменшого за часом), тому з'являються похибки пов'язані з дією сигналів природного походження, що називаються також завадами або збуреннями. Завдання системи навчання - навчити систему термінального керування точному руху об'єкта керування при мінімальному часі відпрацювання корисного сигнала в умовах впливу зовнішніх збурень на процес керування. Відомий спосіб навчання систем термінального керування в умовах завад оснований на використанні швидкодіючих прогнозуючих пристроїв, які будують лінію перемикання сигналу керування в скорішому масштабі часу. З метою формування команди на перемикання сигналу керування в виконавчому пристрої в таких системах використовуються дві моделі: самонастроювана та прогнозуюча. Невідомі параметри об'єкта визначаються за реакцією самонастроюваної моделі. За обраним показником якості знайдені невідомі параметри об'єкта використовуються прогнозуючою моделлю, яка будує прогнозну лінію перемикання. За даними прогнозної моделі та реакції керованого об'єкту на завдання автоматичним оптимізатором формуються команди, за якими здійснюється перемикання сигналу керування виконавчим пристроєм, що забезпечує оптимальне керування об'єктом в процесі випробування [1]. До недоліків такого способу термінального керування відносяться необхідність застосування в 60927 4 системі керування адекватних самонастроюваної та прогнозуючої моделей, а також складність системи, яка пов'язана з застосуванням додаткових елементів системи - прогнозуючої моделі та автоматичного оптимізатора та необхідністю врахування їх дій. Порушення умови адекватності погіршує такі показники системи, як точність відпрацювання та витрати на створення додаткових елементів системи керування. За необхідності врахування порядку математичної моделі складність системи може значно підвищитись без покращання зазначених показників. Найбільш близьким способом, обраним за прототип, є спосіб адаптивного керування з настроюваною моделлю в системах термінального керування, за яким в системі термінального керування попереднє встановлюють вхідні дані, що містять завдання, припустиму похибку відпрацювання завдання об'єктом керування, дані про стан об'єкта керування, величину зсуву координат об'єкта керування, розв'язувальну функцію, початковий сигнал керування в системі, встановлюють також дискретну модель об'єкта керування, довільні значення її початкових вагових коефіцієнтів, а початкові значення її координат встановлюють рівними початковим значенням об'єкта керування, порогові рівні відхилення координат об'єкта керування від моделі, коефіцієнт підсилення алгоритму дискретної корекції, та в процесі руху вимірюють координати об'єкта керування, проводять їх дискретизацію, визначають міру їх відхилення від координат моделі, в разі перевищення міри встановленого порогу проводять корекцію параметрів моделі шляхом додавання до встановлених значень вагових коефіцієнтів результату добутку сигналу керування та сигналу відхилення координат об'єкту керування від моделі, за новими ваговими коефіцієнтами моделі перераховують вагові коефіцієнти розв'язувальної функції. Процес навчання закінчується, коли вимоги за точністю системи управління задовольняються [2]. Недоліком способу навчання, який обраний за прототип, є низька швидкість навчання, за яким встановлення необхідних значень вагових коефіцієнтів здійснюється з широкого інтервалу можливих параметрів. Цей недолік приводить до тривалого настроювання системи керування до бажаної якості. В основу способу підвищення швидкості навчання систем термінального керування в умовах завад за корисною моделлю покладено завдання шляхом усунення недоліків прототипу забезпечити настроювання вагових коефіцієнтів контролера в процесі відпрацювання завдання за рахунок введення в систему керування додаткової процедури щодо уточнення границь інтервалів вибору невідомих параметрів. Результат цієї процедури уточнення меж інтервалів використовується після відпрацювання завдання для зміни значень вагових коефіцієнтів контролера при наступному настроюванні параметрів розв'язувальної функції, що дозволяє підвищити якість алгоритму навчання системи термінального керування за показниками час навчання та точність системи термінального керування - за рахунок звуження інтервалів вибору 5 невідомих параметрів для розв'язувальної функції. Суть способу підвищення швидкості навчання систем термінального керування в умовах завад, при якому в системі керування попередньо встановлюють вхідні дані, що включають завдання, припустиму похибку відпрацювання завдання об'єктом керування, дані про стан об'єкта керування, величину зсуву його координат, встановлюють також розв'язувальну функцію, початкові значення її вагових коефіцієнтів, початковий сигнал керування в системі, встановлюють також і дискретну модель об'єкта з початковим станом, рівним початковому стану об'єкта керування, порогові рівні відхилення координат об'єкта керування від моделі, встановлюють і коефіцієнт підсилення алгоритму дискретної корекції та в процесі руху вимірюють координати об'єкта керування, відхилення поточного стану об'єкта від кінцевого, в разі досягнення похибкою бажаного значення процес керування в системі завершують, в протилежному випадку здійснюють зсув координат об'єкта керування, за зсунутими координатами обчислюють нове значення розв'язувальної функції, за знаком якого визначають сигнал керування в системі, в процесі руху об'єкта також проводять дискретизацію координат об'єкта, визначають міру їх відхилення від координат моделі, якщо відхилення координат об'єкта і моделі перебільшує значення встановленого рівню порогу, то перемножують сигнал керування із сигналами відхилення координат об'єкта керування від моделі та коефіцієнтом підсилення, добуток додають до значень вагових коефіцієнтів настроюваної моделі, здійснюють зміну коефіцієнтів настроюваної моделі за результатами обчислення, перераховують коефіцієнти моделі в вагові коефіцієнти розв'язувальної функції, полягає в тому, що в системі термінального керування додатково на етапі підготовки вхідних даних встановлюються границі інтервалу припустимих параметрів, вводиться процедура уточнення границь параметрів дискретної моделі, в межах одного кроку випробування системи відбувається корекція вагових коефіцієнтів дискретної моделі, за результатами корекції вагових параметрів моделі перераховують вагові коефіцієнти розв'язувальної функції. Суть корисної моделі полягає і в тому, що в межах кроку випробування системи керування формується набір параметрів дискретної моделі, серед сформованого набору визначають мінімальне та максимальне значення параметрів, при цьому значення нижньої границі інтервалу переносять в нове більше значення, якщо старе значення нижньої границі менше за нове, а значення верхньої границі інтервалу переносять в нове менше значення, якщо старе значення більше за нове значення. Суть корисної моделі полягає також і в тому, що по завершенню кроку випробування системи керування вибір параметрів дискретної моделі відбувається з нового, уточненого інтервалу параметрів. Порівняльний аналіз способу, який заявляється, із прототипом дозволяє дійти висновку, що спосіб підвищення швидкості навчання систем термінального керування в умовах завад відрізняється тим, що при встановленні вхідних даних в 60927 6 системі керування додатково вводяться границі інтервалу параметрів дискретної моделі об'єкта керування та процедура уточнення границь, після завершення випробування та в разі недосягнутості мети навчання проводиться вибір параметрів дискретної моделі для подальшої корекції як за алгоритмом навчання, так і за алгоритмом дискретної корекції з нового інтервалу параметрів, що визначений після уточнення границь інтервалу. На заключній стадії формування поточного сигналу керування при обчисленні розв'язувальної функції використовують нові значення вагових коефіцієнтів, що розраховані на останньому кроку випробування. Таким чином, спосіб підвищення швидкості навчання систем термінального керування в умовах завад, який заявляється, відповідає критерію винаходу "новизна". Суть способу пояснюється за допомогою ілюстрацій, на Фіг. 1 показано послідовність дій виконання способу, що заявляється, на Фіг. 2 приведено структурну схему пристрою, що реалізує спосіб, який заявляється, на Фіг. 3 представлений розгорнутий вигляд блок-схем и пристрою, що реалізує спосіб, який заявляється, на Фіг. 4 показано динаміку об'єкта керування з початковою установкою коефіцієнтів без адаптації в ковзному режимі для випадку вимірювання двох координат у площині положення-швидкість, на Фіг. 5 показано той же ковзний режим об'єкта керування у часовій площині, на Фіг. 6 показано сигнал керування у цьому режимі, на Фіг. 7 показано перехідний процес, який отриманий після процесу навчання термінальному керуванню, на Фіг. 8 показано зміну настоюваних параметрів виключно за процедурою навчання, на Фіг. 9 показано зміну настоюваних параметрів за процедурою навчання та процедурою настроювання параметрів дискретної моделі, на Фіг. 10 показано зміну настоюваних параметрів з врахуванням процедури уточнення границь, на Фіг. 11 показано зміну розмірів областей настроюваних параметрів. Послідовність виконання дій в способі підвищення швидкості навчання систем термінального керування в умовах завад пояснюється схемою на Фіг. 1, де показано, що перед початком функціонування в системі керування встановлюють вхідні дані, які складаються з завдання, припустимої похибки  відпрацювання завдання динамічним об'єктом, початкового стану X0  об'єкта керування, величини зсуву координат N , розв'язувальної функції Fc, Xt  , початкового вектора її вагових коефіцієнтів c 0 , початкового сигналу керування u0 на вході об'єкта керування, дискретної моделі об'єкта керування, дані про початковий стан моделі Xм 0 , припустимі значення відхилень координат і моделі, коефіцієнту підсилення  алгоритму дискретної корекції, границі інтервалів параметрів. Далі, в процесі настроювання дають чергове випробування системи термінального керування, при якому об'єкт керування здійснює рух в кінцевий стан. В процесі руху вимірюють не тільки коорди 7 нати Xt  динамічного об'єкта, а ще й додатково контролюють координати еталонної моделі Xм t  . При цьому обчислюється похибка t  відхилення координат xi t  динамічного об'єкта від кінцевого стану xi tк  . В разі дії завад здійснюють зсув координат об'єкта керування на величини Ni , за зсунутими координатами обчислюють значення розв'язувальної функції Fct , Xt  . Визначають знак сигналу керування на вході об'єкта керування таким, що відповідає знаку розрахованого значення розв'язувальної функції Fct , Xt  . Якщо похибка t  відхилення координат xi t  динамічного об'єкта відмінна від нуля, то проводять дискретизацію вихідних сигналів об'єкта керування. За дискретними даними координат xi t  динамічного об'єкта та еталонної моделі Xм t  обчислюється відхилення координат динамічного об'єкта від координат еталонної моделі t  . В разі виявлення відхилення координати t  від встановленого рівня порогу сигналу відхилення t  його перемножують зі значенням поточного управління ut  , отриманий добуток з коефіцієнтом підсилення  додають до початкового вектора настроюваних параметрів  та визначають нові параметри дискретної моделі. Встановлюють нові параметри  настроюваної моделі. Для нових значень  розраховують вагові коефіцієнти ci t  розв'язувальної функції Fct , Xt  , за якими обчислюють її нове значення. Далі за знаком значення функції Fct , Xt  обчислюють сигнал керування ut  для даного моменту часу керування t . На заключній стадії настроювання в разі невідповідності значень похибки t  її порогу  проводиться подальше обчислення сигналу управління для нових координат поточного стану динамічного об'єкту управління Xt  та еталонної моделі Xм t  . В разі недосягнення мети навчання проводять процедуру уточнення границь інтервалів припустимих значень дискретної моделі, нові початкові параметри моделі вибирають з нових інтервалів. Нові значення моделі перераховують у параметри розв'язувальної функції. Проводять їх корекцію за алгоритмом навчання. Повторюють процес навчання в системі термінального керування на новому кроку випробування. Спосіб настроювання системи адаптивного термінального керування при керуванні динамічним об'єктом реалізується за допомогою пристрою, який містить (див. Фіг. 2, Фіг. 3), як варіант конструктивного виконання, виконавчу частину 1, що складається з контролера 2, релейного елемента 3 перетворювача вагових коефіцієнтів контролера 4, об'єкта керування 5, вимірювального каналу об'єкта керування 6, що складається з датчика положення 7, датчика швидкості 8, з блоку зсуву координат 9, таймера 13, ключа для сигналу керу 60927 8 вання 10, ключів для сигналів датчиків 11, 12, механізму адаптації 14, до якого входять блок дискретної моделі 15, що складається з формувача значень початкових координат моделі 16 та формувачів значень координат положення дискретної моделі 17 та значень координат швидкості 18, блок розрахунку параметрів моделі 19, що складається з обчислювачів відхилень координат положення об'єкта керування від дискретної моделі 20 та швидкості 21, обчислювачів параметрів моделі 22 та 23, блок уточнення параметрів границь 24, що складається з пристроїв уточнення границь зміни коефіцієнта дискретної координати положення 26 та уточнення границь зміни коефіцієнта дискретної координати швидкість 27 дискретної моделі, та пристрою вибору нових параметрів 25. Конструктивно вихід контролера 2 зв'язаний зі входом об'єкта керування 5 через релейний елемент 3. Вихід релейного елементу 3 додатково зв'язаний зі входом ключа 10 та входом моделі 17. Вихід об'єкта керування 5 конструктивно зв'язаний зі входами блоку зсуву координат 9 через датчики положення 7 та швидкості 8. Виходи блоку 9 зв'язані з інформаційними входами контролера 2 та зі входами ключів 11, 12. Виходи датчиків положення 7 та швидкості 8 конструктивно зв'язані з сигнальними входами контролера 2 через блок зсуву координат 9. Вихід таймера 13 конструктивно зв'язаний зі входами керування ключів 10, 11, 12. Виходи ключів 11, 12 конструктивно зв'язані зі входами обчислювачів відхилень координат 20, 21, а вихід ключа 10 зв'язаний зі входами обчислювачів параметрів моделі 22, 23. Вихід формувача початкових значень моделі 16 конструктивно зв'язаний зі входами формувачів координат моделі 17, 18, при цьому вихід формувача координат положення 17 конструктивно зв'язаний зі входом формувача координат швидкості моделі 18. Виходи формувачів координат моделі 17, 18 конструктивно зв'язані зі входами обчислювачів параметрів моделі 22, 23 через обчислювачі відхилень 20, 21 блоку розрахунку параметрів моделі 19. Виходи блоків обчислювачів 22, 23 конструктивно зв'язані зі входами формувачів координат моделі 17, 18 відповідно та входами пристроїв уточнення границь зміни коефіцієнта дискретної координати положення 26 та уточнення границь зміни коефіцієнта дискретної координати швидкість 27 дискретної моделі, та пристрою вибору нових параметрів 25 блоку уточнення параметрів границь 24. Виходи пристрою вибору нових параметрів 25 конструктивно зв'язані зі входами контролера 2 через блок перетворювача вагових коефіцієнтів контролера 4 виконавчого блоку 1 системи. Пристрій, за допомогою якого реалізується спосіб адаптивного управління в системах термінального управління при керуванні динамічним об'єктом, працює таким чином. Перед початком роботи системи керування (див. Фіг. 2, Фіг. 3) для об'єкта, що знаходиться в початковому стані X0  , встановлюють завдання X з припустиме значення похибки  відпрацювання завдання та значення координат початкового стану дискретної моделі Xм 0 . Встановлюють 9 60927 10 також довільні значення вагових коефіцієнтів контролера 2 с 0 . Момент часу t подачі команди «Пуск» на систему керування вважають за початковий, тобто t  0 . Команда «Пуск» подається також на дискретну модель 15. З моменту t  0 починається розрахунок похибки за положенням та швидкістю динамічного об'єкта за допомогою датчиків 7, 8 і формування значень координат моделі за допомогою формувачів значень координат положення 17 та швидкості дискретної моделі 18. Перед здійсненням обчислення відхилення координат об'єкта та моделі здійснюється зсув координат об'єкта керування в блоку 9 на величину N . Цей зсув дозволяє виключити вплив неконтрольованих похибок на роботу системи термінального керування. Зсув здійснюється в напрямку протилежному поточним змінам координат об'єкта керування. Далі значення координат об'єкта керування поступають на блоки обчислення відхилення координат об'єкта від відповідних координат моделі 20, 21. Значення координат динамічного об'єкта з виходу блоків 7, 8 поступають також на сигнальні входи контролера 2. Контролер 2 за даними с 0 і координат об'єкта керування. При русі динамічного об'єкта результат множення сигналів керування, відхилень координат об'єкту та дискретної моделі з постійним коефіцієнтом  з блоків множення 22, 23 як значення нових параметрів подається на входи формувачів 17, 18 моделі 15 та входи пристроїв уточнення границь зміни коефіцієнта дискретної координати положення 26 та уточнення границь зміни коефіцієнта дискретної координати швидкість 27 дискретної моделі. Дискретна модель об'єкта керування представлена рівняннями виду xj  2xj  1  xj  2  1uj  1  uj  2, (4)   xj  xj  1  2uj  1.  xt  , xt  обчислює значення розв'язувальної функції Fc, Xt  , яка в фазовому просторі має назву поверхні перемикань, де Xt  - вектор, компоненти  якого складаються з сигналів xt  і xt  . Знак функції Fc, Xt  буде визначати знак сигналу керу i n  i n  1   n   u1n  1 , (5) де i  12 . , Правило (5) діє кожного разу, коли відхилення координат об'єкта керування та моделі n пере вання ut  в поточний момент часу t . Сигнал керування формується релейним елементом 3, а саме вищує обрану величину порогу  . Вимір такої величини відхилення здійснюється безперервно протягом відпрацювання завдання шляхом порівняння двох сусідніх малих інтервалів часу n  1T,nT . Так, якщо n  n  1 корекція кое   U, якщо Fc, Xt   ,  ut     U, якщо Fc, Xt   , (1) Ut  0 , якщо Fc, Xt   .  Мала величина  введена в закон управління (1) для виключення похибок округлення та усікання при обчисленні на ЕОМ. Релейний елемент комутує напругу величиною U або U на вхід динамічного об'єкта 5 за законом (1). В (1) третій вираз в правій частині означає, що значення керуючої дії ut  зберігається рівним попередньому значенню, навіть якщо фазові координати об'єкта керування знаходяться на лінії перемикання, тобто якщо Fc, Xt   0 . Керуюча дія ut  з моменту t  0 до кінцевого tк примушує об'єкт рухатися в сторону зменшення похибки t   xз  xt  . Результати, які представлені на Фіг. 4-8, моделювалися для випадку регулятора з двома невідомими параметрами, тобто для вирішувальної функції   Fc, Xt   c1xt   c 2 xt  xt . (2) В (1), (2) використовуються координати, які є зсунутими на величину N за правилом Xt   N, якщо Fc, Xt   , (3) Xt    Xt   N, якщо Fc, Xt   , де Xt   x1t , x t T  2 - вектор вимірюваних В рівняннях (4) x, x і u - вимірювані зна    чення координат об'єкта керування і сигналу керування на j-му інтервалі часу, 1,2 - оцінювані параметри моделі. В разі виявлення відхилень координат моделі та об'єкта керування більших за встановлені порогові значення  обчислювачі 22, 23 здійснюють розрахунок нових параметрів дискретної моделі за правилом   фіцієнтів  за правилом (5) не відбувається, у протилежному випадку завжди відбувається корекція вектора  . Після виконання операції (5) отримуються оцінки координат вектора  , за якими відбувається розрахунок складових вектора c для подальшого їх використання в законі (2), c1  1T 1, c 2  2211T 1 , (6) де 1,2 - обчислені значення вектору параметрів дискретної моделі за правилом (4). На наступному кроці навчання зміна параметрів розв'язувальної функції здійснюється так  cn1, X  ,  cn  PrSk cn1  X якщо X   та N  2, (7) , Pr c ,   Sk n1  X  якщо X   nf N  2. Якщо вимірювані координати X  об'єкта в процесі керування попадають в область цілі  з однією зміною знака сигналу керування ut  , то зміни параметрів c не відбувається, що показує перший вираз в правій частині (7). У випадку, коли за одну зміну знака сигналу керування ut  координати об'єкта керування не попадають в область  , тоді відбувається зміна параметрів c за другим виразом в правій частині (7). Третій вираз в правій частині (7) справедливий у випадку, якщо процес керування іде в ковзному режимі (з вели 11 60927 кою кількістю зміни знака сигналу керування). При цьому, якщо нові значення c виходять за межі їх припустимих інтервалів, які визначаються областю Sk , то в результаті операції проектування PrS здійснюється їх виправлення так, що нові параметри знаходяться усередині області Sk або на її границі. Уточнення границь множини допустимих параметрів для (2), (5) здійснюється шляхом перебору оцінок i , які було отримано на j-му кроці випробування i i  max вik , ji  min вk (8) j 0 k  j 0 k  j Вибір початкової оцінки  0  на наступному кроці навчання здійснюється з інтервалу i i  i 0   i (9) та їх зворотному перерахунку за формулами (6). Процедура уточнення границь (9) утворює ряд областей Sk припустимих параметрів c таких, що кожна наступна Sn менша за розмірами попередньої Sn 1 , тобто Sn  Sn1 . Робота системи закінчується, якщо задовольняється вимога влучення координат об'єкту в кін    цевий стан     x1 , x  (див. Фіг. 7). Типовий 2 характер зміни вагових коефіцієнтів c n в процесі керування за рахунок тільки процедури навчання (7) показаний на Фіг. 8, за рахунок взаємодії процедури навчання та процедури дискретного оцінювання параметрів (5) представлений на Фіг. 9, а при повній роботі алгоритму, що додатково включає й уточнення границь параметрів, показаний на Фіг. 10. Дія процедури уточнення множини припус   k k k тимих параметрів Sk  c1 , c1  c k , c 2 2  показана на Фіг. 11. Ефективність дії способу, що заявляється, можна відстежити за результатами випробування, які наведені на Фіг. 4-8. В експерименті було задіяний об'єкт керування, для якого функція (2) має параметри c T  1 0,5 . Передбачалося, що коор, динати початкового стану об'єкта керування XT 0   2, 0 в усіх випадках випробувань обираються однаковими. На Фіг. 4 показано динаміку об'єкта керування з початковим встановленням T коефіцієнтів c 0  20, 70 без адаптації (перший крок навчання, без впливу дискретного алгоритму та алгоритму уточнення границь параметрів), що відповідає ковзному режиму при вимірюванні двох координат у площині положення-швидкість. На Фіг. 5, Фіг. 6 показаний той же ковзний режим об'єкта керування у часовій площині та сигнал керування для цього режиму, який викликаний помилковим встановленням коефіцієнтів у векторі параметрів c . На Фіг. 7 показаний процес адаптації параметрів вирішувальної функції, в результаті якого мож 12 на оцінити вплив дії алгоритму на процес керування. Так за дією алгоритму час керування зменшено на 33 %. За алгоритмом навчання (7) в процесі випроT бувань отриманий вектор c 34  6177, 32,41 за , n  34 кроків навчання (див. Фіг. 8), ефект впливу алгоритму навчання (7) та дискретного настроювання параметрів моделі (5) представлений на Фіг. 9, в результаті якого отриманий вектор c T  40,68, 22,17 за n  20 кроків навчання. На 20 Фіг. 10 показано ефект впливу процедури уточнення границь (8) на процес навчання, що привело до T отримання вектора c 8  16,87, 8,28 за n  8 кро ків навчання. Оціночний вектор c  приведений до вихідного має вид c  1 0,49 . Швидкість навчан, ня підвищена у 4,25 рази. Така швидкість навчання отримана за рахунок ускладнення алгоритму, що включає алгоритм дискретного оцінювання (5) та уточнення границь (8). В процесі навчання границі уточнювались 5 разів, при цьому S5  S4  S3  S2  S1 , остання множина припустимих параметрів має вид c S5  16,04,16,87 8,28, 89,19 (див. Фіг. 11). На відміну від системи керування з [1] в способі, що заявляється, маємо усталений процес керування без введення додаткових елементів стабілізації руху. Підвищення ефективності застосування способу адаптивного керування з налаштованою моделлю в системах термінального керування, який заявляється, у порівнянні з прототипом, полягає в тому, що на відміну від прототипу в способі, що заявляється, дозволяється підвищити швидкість навчання, яка вимірюється кількістю послідовних кроків навчання, при цьому встановлення необхідних значень вагових коефіцієнтів здійснюється зі звуженого інтервалу можливих параметрів. Інтервали уточнюються на кожному кроці навчання, що в результаті приводить до зменшення кількості окремих кроків настроювання системи керування до бажаної якості. Джерела інформації: 1. Адаптивные системы идентификации // [Кику А. Г., Костюк В. И., Краскевич В. Е. и др.]; под ред. В. И. Костюка. - К.: Тэхника, 1975. - 288 с. аналог. 2. Пат. 54135 Україна, МПК (2009) G05B 13/00, G05B 11/00. Спосіб адаптивного керування з настроюваною моделлю в системах термінального керування/ Кучеров Д. П., Іванов Б. П., Мельник О. Д., Чікалов М. А., Копилова З. М., Кузьменко Т. П.; заявники та патентовласники Кучеров Д. П., Іванов Б. П., Мельник О. Д., Чікалов М. А., Копилова З. М., Кузьменко Т. П. - № u 2010 05554; заявл. 07.05.10; опубл. 25.10.10, Бюл. 20. - прототип. 13 60927 14 15 60927 16 17 60927 18 19 Комп’ютерна верстка А. Крулевський 60927 Підписне 20 Тираж 24 прим. Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601