Спосіб створення еталонів плоских перерізів тривимірних зеренних структур металевих матеріалів з визначеним розподілом розмірів тривимірних зерен
Номер патенту: 113112
Опубліковано: 12.12.2016
Автори: Даніленко Тетяна Петрівна, Даниленко Едуард Іванович
Формула / Реферат
1. Спосіб створення еталонів плоских перерізів тривимірних зеренних структур металевих матеріалів з визначеним розподілом розмірів тривимірних зерен, який полягає в тому, що виготовляють шліф, отримують видиме зображення зеренної структури металу, для урахування форми плоских перерізів зерен визначають коефіцієнти їх форми bi, для чого вибирають мінімальну статистично необхідну кількість типових за формою плоских перерізів, наносять на всю площину кожного з них під рівним кутом одна до другої не менше 8-ми груп паралельних рівновіддалених січних, вимірюють хорди, що утворилися в результаті перерізу січних межами цих типових плоских перерізів зерен, розподіляють заміряні хорди у відносних частках по розмірних інтервалах у заданій розмірній шкалі, знаходять для кожного розмірного інтервалу середні відносні частки хорд Рk(![]() )ср від цих типових плоских перерізів зерен і визначають коефіцієнти форми bi для кожного розмірного інтервалу шкали з відношення знайдених середніх відносних часток хорд від плоских перерізів зерен до відповідних розрахованих відносних часток хорд від кола; для урахування форми тривимірних зерен визначають коефіцієнти форми ai, для чого вибирають мінімальну статистично необхідну кількість типових за формою максимальних плоских перерізів зерен, присутніх на зображенні структури, наносять на всю площину кожного з них під рівним кутом одна до другої не менше 8-ми груп паралельних рівновіддалених січних, вимірюють хорди, що утворилися в результаті перерізу січних межами цих типових максимальних плоских перерізів зерен, розподіляють заміряні хорди у частках по розмірних інтервалах у заданій розмірній шкалі, знаходять для кожного розмірного інтервалу середні відносні частки хорд Рk(
)ср від цих типових плоских перерізів зерен і визначають коефіцієнти форми bi для кожного розмірного інтервалу шкали з відношення знайдених середніх відносних часток хорд від плоских перерізів зерен до відповідних розрахованих відносних часток хорд від кола; для урахування форми тривимірних зерен визначають коефіцієнти форми ai, для чого вибирають мінімальну статистично необхідну кількість типових за формою максимальних плоских перерізів зерен, присутніх на зображенні структури, наносять на всю площину кожного з них під рівним кутом одна до другої не менше 8-ми груп паралельних рівновіддалених січних, вимірюють хорди, що утворилися в результаті перерізу січних межами цих типових максимальних плоских перерізів зерен, розподіляють заміряні хорди у частках по розмірних інтервалах у заданій розмірній шкалі, знаходять для кожного розмірного інтервалу середні відносні частки хорд Рk(![]() )ср від цих типових максимальних плоских перерізів зерен і визначають коефіцієнти форми ai для кожного розмірного інтервалу шкали з відношення знайдених середніх відносних часток хорд від цих типових максимальних плоских перерізів зерен до відповідних розрахованих відносних часток діаметрів плоских перерізів (кіл) від сфери, після чого здійснюють реконструкцію розподілу Pk(d) розмірів плоских перерізів зерен; який відрізняється тим, що визначення коефіцієнтів форми bi і ai здійснюють з урахуванням того, що від плоского перерізу зерна k-го розмірного інтервалу отримуються хорди тільки в розмірні інтервали від k-го до першого; а як вихідну інформацію для реконструкції розподілу Pk(d) розмірів плоских перерізів зерен вибирають необхідний для еталона розподіл P(Dk) розмірів тривимірних об'ємних зерен у заданій розмірній шкалі і реконструкцію розподілу розмірів їх плоских перерізів Pk(d) здійснюють шляхом вирішення лінійних рівнянь виду:
)ср від цих типових максимальних плоских перерізів зерен і визначають коефіцієнти форми ai для кожного розмірного інтервалу шкали з відношення знайдених середніх відносних часток хорд від цих типових максимальних плоских перерізів зерен до відповідних розрахованих відносних часток діаметрів плоских перерізів (кіл) від сфери, після чого здійснюють реконструкцію розподілу Pk(d) розмірів плоских перерізів зерен; який відрізняється тим, що визначення коефіцієнтів форми bi і ai здійснюють з урахуванням того, що від плоского перерізу зерна k-го розмірного інтервалу отримуються хорди тільки в розмірні інтервали від k-го до першого; а як вихідну інформацію для реконструкції розподілу Pk(d) розмірів плоских перерізів зерен вибирають необхідний для еталона розподіл P(Dk) розмірів тривимірних об'ємних зерен у заданій розмірній шкалі і реконструкцію розподілу розмірів їх плоских перерізів Pk(d) здійснюють шляхом вирішення лінійних рівнянь виду:
![]()
де: n - кількість розмірних інтервалів у розмірній шкалі;
k - порядковий номер розмірного інтервалу від 1-го до n-го;
dk; dk-1 - діаметри кіл, рівновеликих плоским перерізам зерен, відповідно, k-го, (k-1)-го розмірних інтервалів; одиниці довжини;
Dk; Dk+1;..., Dn - діаметри сфер, рівновеликих тривимірним зернам, відповідно, k-го, (k+1)-го,..., n-го розмірних інтервалів; одиниці довжини;
Pk(d) - відносна частка плоских перерізів зерен k-го розмірного інтервалу;
P(Dk); P(Dk+1);...; P(Dn) відносні частки тривимірних зерен еталона, відповідно, k-го, (k+1)-го,..., n-го розмірних інтервалів;
aa; ab;...; af - коефіцієнти форми тривимірних зерен; після чого отримують нормовані значення Pk'(d) з відношення 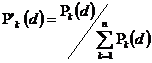 ; потім, використовуючи як вихідну інформацію, отриманий нормований розподіл Pk'(d) розмірів плоских перерізів здійснюють реконструкцію розподілу довжин хорд Рk(
; потім, використовуючи як вихідну інформацію, отриманий нормований розподіл Pk'(d) розмірів плоских перерізів здійснюють реконструкцію розподілу довжин хорд Рk(![]() ) шляхом вирішення лінійних рівнянь виду:
) шляхом вирішення лінійних рівнянь виду:
![]() , де: n - кількість розмірних інтервалів у розмірній шкалі;
, де: n - кількість розмірних інтервалів у розмірній шкалі;
k - порядковий номер розмірного інтервалу від 1-го до n-го;
![]() - довжини хорд k-го і (k-1)-го розмірних інтервалів; одиниці довжини;
- довжини хорд k-го і (k-1)-го розмірних інтервалів; одиниці довжини;
dk; dk+1;...; dn - діаметри кіл, рівновеликих плоским перерізам зерен, відповідно, k-гo, (k+1)-го,..., n-го розмірних інтервалів; одиниці довжини;
Рk(![]() ) - відносна частка хорд k-го розмірного інтервалу;
) - відносна частка хорд k-го розмірного інтервалу;
P'k(d); P'k+1(d);...; P'n(d) - нормовані відносні частки плоских перерізів зерен, відповідно, k-го, (k+1)-го,..., n-го розмірних інтервалів;
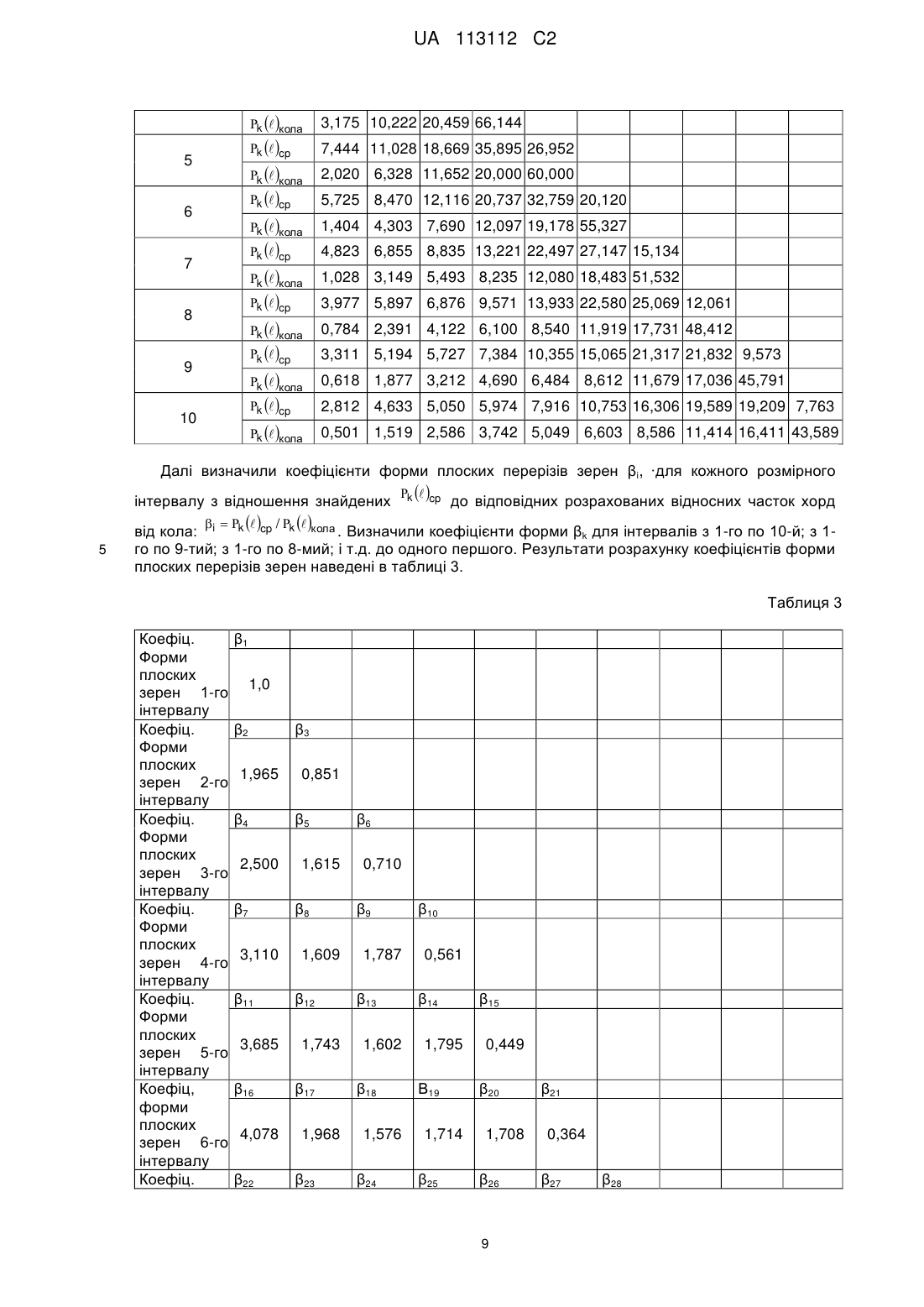
ba; bb;...; βf - коефіцієнти форми плоских перерізів зерен;
після чого отримують нормовані значення Рk(![]() ) з відношення
) з відношення 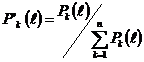 ;
;
за отриманим розподілом розмірів плоских перерізів зерен Pk'(d) створюють еталон плоского перерізу зеренної структури у вигляді кола із схематизованою сіткою, яка обмежує розміри зерен, або приймаючи за еталон сам розподіл розмірів плоских перерізів зерен Pk'(d);
виходячи з розподілів розмірів тривимірних зерен P(Dk), їх плоских перерізів Pk'(d) і розподілу хорд Рk'(![]() ) знаходять числові характеристики основних параметрів тривимірної зеренної структури, її плоского перерізу і розподілу хорд.
) знаходять числові характеристики основних параметрів тривимірної зеренної структури, її плоского перерізу і розподілу хорд.
2. Спосіб за п. 1, який відрізняється тим, що видимим зображенням структури може бути зображення плоских перерізів будь-яких елементів структури сферичної (в цьому випадку коефіцієнти форми ai і βi дорівнюють одиниці), поліедричної, еліпсоїдної та подібних їм форм, в тому числі неметалевих включень, графітної і цементитної фаз, вторинних фаз, інтерметалевих фаз та ін., для яких знаходять відповідні коефіцієнти форми їх плоских перерізів βі і коефіцієнти форми самих тривимірних елементів структури ai і створюють еталони плоских перерізів цих структур.
3. Спосіб за п. 1, який відрізняється тим, що для моделювання співвідношення розподілів розмірів тривимірних зерен P(Dk) і встановлення відповідних їм розподілів плоских перерізів Pk'(d) і розподілів хорд Рk'(![]() ) вибирають будь-який розподіл розмірів тривимірних зерен P(Dk).
) вибирають будь-який розподіл розмірів тривимірних зерен P(Dk).
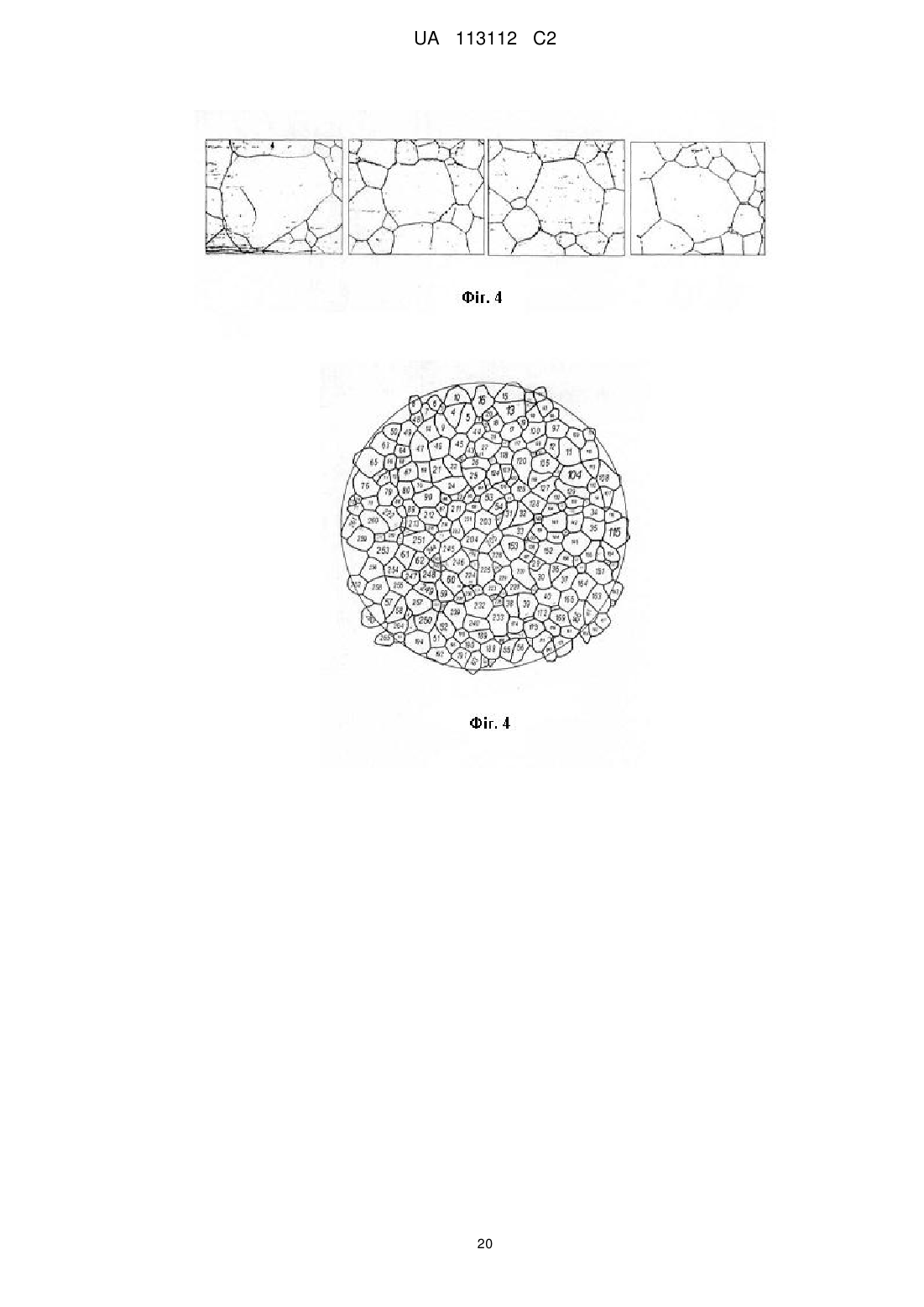
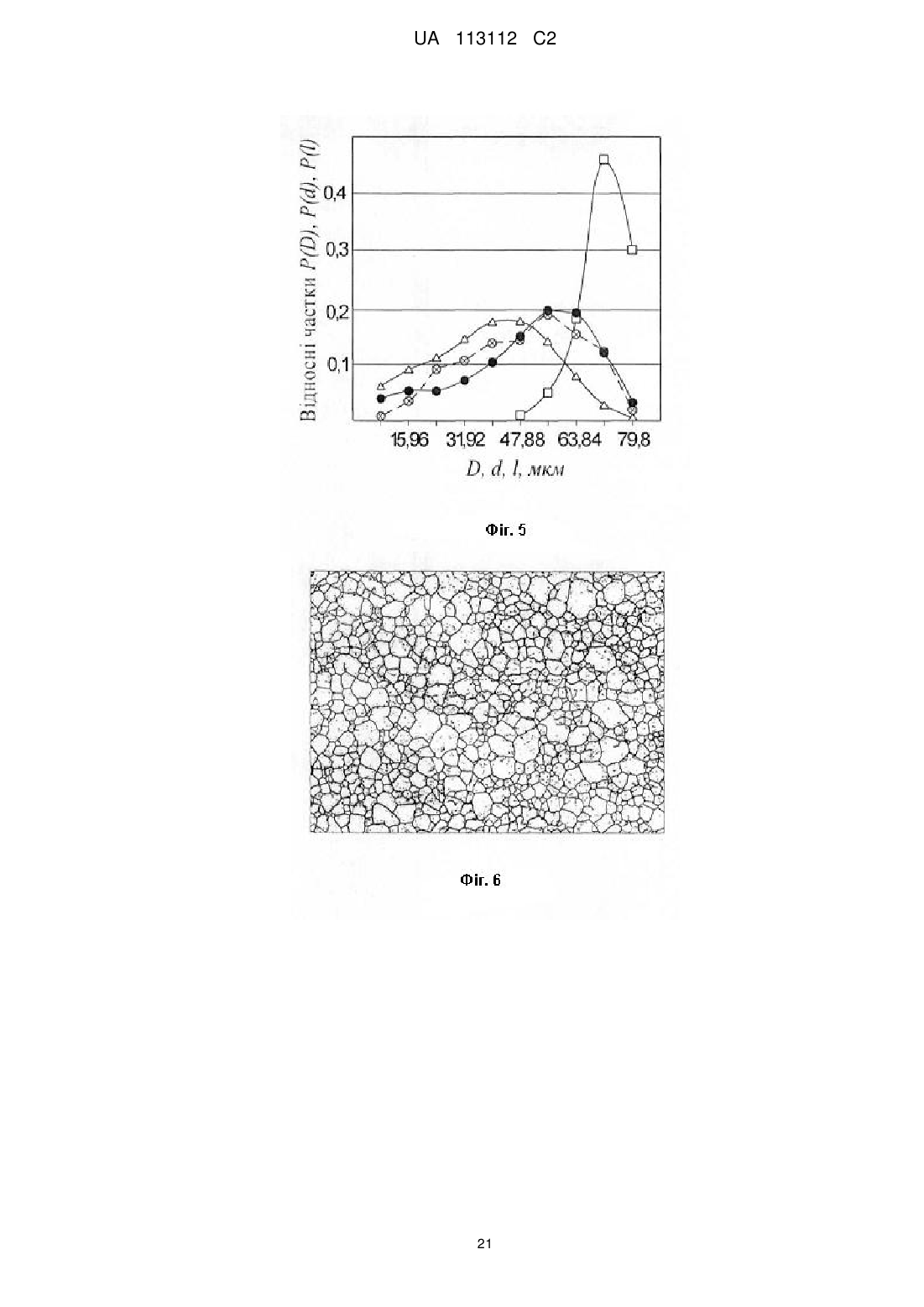
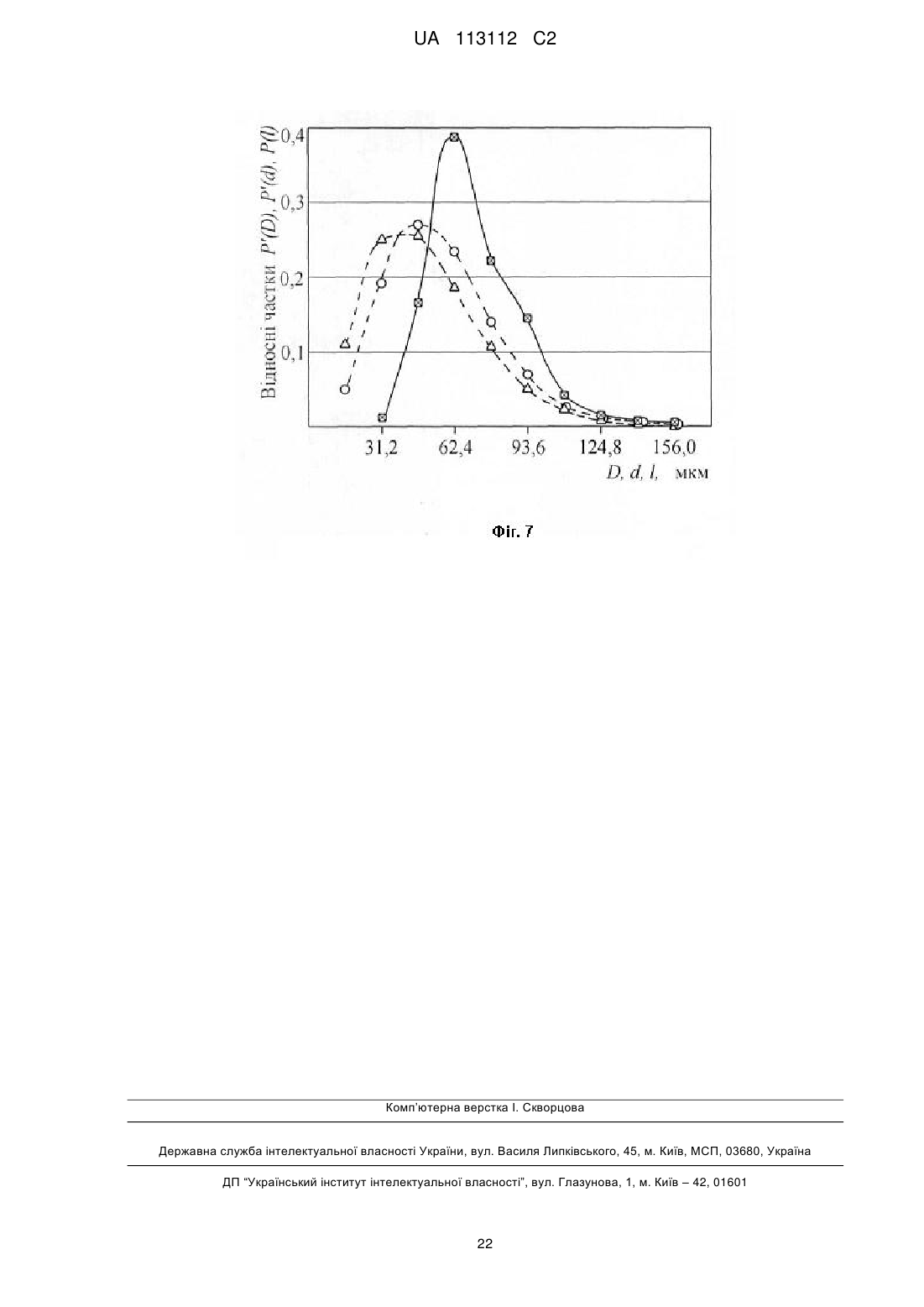
Текст
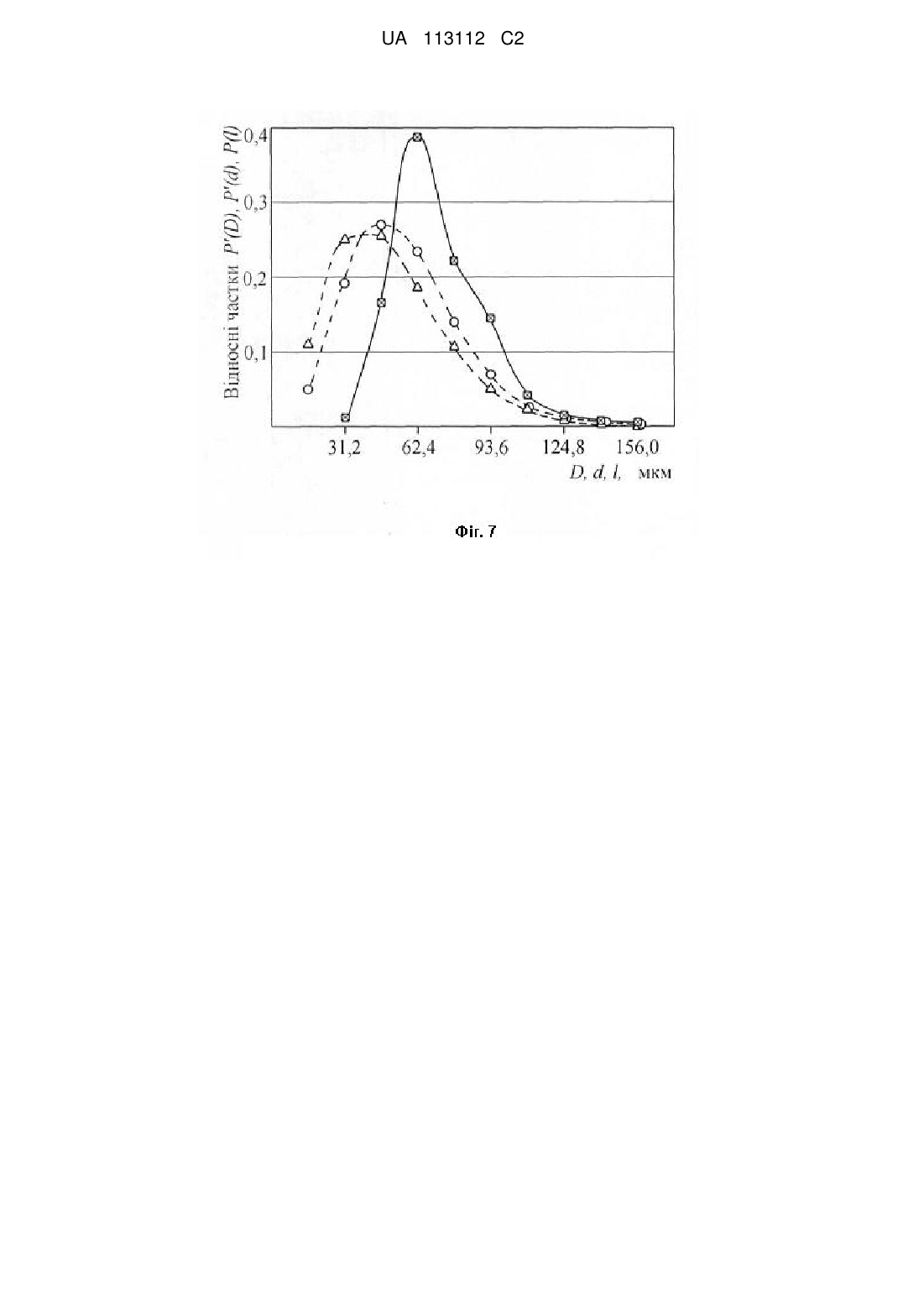
Реферат: Спосіб створення еталонів плоских перерізів тривимірних зеренних структур металевих матеріалів з визначеним розподілом розмірів тривимірних зерен належить до області металографічних досліджень і аналізу зеренної структури металевих матеріалів, способів визначення основних її параметрів, стереологічної реконструкції структури. Спосіб базується на реконструкції розподілу розмірів плоских перерізів, виходячи із заздалегідь вибраного розподілу розмірів тривимірних зерен і може бути застосований до створення еталонів плоских перерізів будь-яких елементів структури сферичної, поліедричної, еліпсоїдної та подібних їм форм, в тому числі неметалевих включень, графітної і цементитної фаз, вторинних фаз, інтерметалевих фаз та ін. Спосіб дозволяє підвищити точність створеного еталона при одночасному забезпеченні розширення його технологічних можливостей, що збільшує коло його практичного застосування. UA 113112 C2 (12) UA 113112 C2 UA 113112 C2 5 10 15 20 25 30 35 40 45 50 55 60 Винахід належить до області металографічних досліджень і аналізу зеренної структури металевих матеріалів, способів визначення основних її параметрів, стереологічної реконструкції структури. Зазвичай металеві зеренні структури являють собою полідисперсні системи, тобто такі, що складаються із зерен різних розмірів. Найважливішою вихідною характеристикою таких полідисперсних систем є розподіл їх розмірів, який дозволяє розрахувати багато інших важливих кількісних параметрів структури: середній, максимальний, модальний розмір зерен, кількість зерен в одиниці об'єму (наприклад, в 1 мм), характеристики неоднорідності (розкиданості) розмірів - середньоквадратичне відхилення від середнього розміру, коефіцієнт варіації розподілу розмірів зерен та ін. Через непрозорість металів для світла їх структуру найчастіше досліджують на металографічному шліфі, де зеренна структура представлена сукупністю багатокутників, якими є плоскі перерізи тривимірних (об'ємних) зерен, що мають форму різноманітних поліедрів (С.А.Салтыков. Стереометрическая металлография. - Μ., 1970. - С. 276-286). Але цей плоский переріз на шліфі є двовимірним зображенням реально існуючої тривимірної структури, саме яка і впливає на властивості металопродукції. Тому задача формування певної структури, наприклад з регламентованим середнім розміром зерен, є важливою і актуальною, і для її вирішення необхідно якомога достовірніше визначати параметри саме тривимірної зеренної структури. Однак, оскільки непрозорість металевих матеріалів для світла не дозволяє безпосередньо досліджувати тривимірні структури, то у стандартах з визначення величини зерна одним із методів є метод візуального порівняння двовимірної структури на шліфі, тобто сукупності плоских перерізів тривимірних зерен, з еталонними шкалами плоских перерізів зеренних структур. Відомий спосіб, згідно з яким, вісімнадцять еталонів плоских перерізів зеренної структури створені у вигляді кола із схематизованою сіткою, яка обмежує розміри зерен (ГОСТ 5639-82: Стали и сплави. Методы выявления и определения величины зерна. - М., 1983. 21 с). Еталони представлені в основних і додаткових шкалах. Кожному еталону відповідає номер зерна G. Еталони складені так, що при збільшенні зображення у 100 разів номер зерна G відповідає G 2 числовим показникам величини зерна згідно з рівнянням m=82 , де m - кількість зерен на 1 мм площі металографічного шліфа. З цими еталонами порівнюють видимі під мікроскопом плоскі перерізи реальних структур і визначають середню величину зерен цієї реальної структури у вигляді номера зерна G, якому відповідають певні числові характеристики структури, а саме середня площа плоских перерізів зерен а, середнє число плоских перерізів зерен m на площі 1 2 мм , середній діаметр плоских перерізів зерен dm, середній умовний діаметр зерна dL, який по суті є середньою довжиною хорд, отриманих в результаті нанесення на зображення структури січних ліній і перерізу цих ліній межами зерен тощо. Недоліком даного способу є те, що його еталони не надають інформації про тривимірну структуру, плоский переріз якої відповідав би схематизованій сітці кожного еталона. Тому цей спосіб не дає можливості визначити розподіл розмірів тривимірних зерен реальних структур і на його основі розрахувати багато інших важливих кількісних параметрів тривимірної структури: середній, максимальний, модальний розмір тривимірних зерен, кількість зерен в одиниці об'єму 3 (наприклад, в 1 мм ), характеристики неоднорідності розмірів середньоквадратичне відхилення від середнього розміру, коефіцієнт варіації розподілу розмірів зерен та ін. Відомий також спосіб, згідно з яким двадцять п'ять еталонів плоских перерізів зеренної структури створені у вигляді кола із схематизованою сіткою, яка обмежує розміри зерен (ISO 643:2012. Steels-Micrographic determination of the apparent grain size. British Standards Institution, 2015. - 44 p.). Принципи створення еталонів ті ж, що і в попередньому способі, тому йому притаманні ті ж недоліки. Збільшення кількості еталонів не дає можливості визначити кількісні параметри реально існуючої тривимірної структури, саме яка і впливає на властивості металевих виробів. Найбільш близьким за змістом є спосіб визначення основних параметрів об'ємної структури металевих матеріалів (Патент України № 97453. - Опубл. 2012 - Бюл. № 3), який полягає в тому, що виготовляють шліф, отримують видиме зображення зеренної структури металу, для урахування форми плоских перерізів зерен визначають коефіцієнти їх форми β i, для чого вибирають мінімальну статистично необхідну кількість типових за формою плоских перерізів, наносять на всю площину кожного з них під рівним кутом одна до другої не менше 8-ми груп паралельних рівновіддалених січних, вимірюють хорди, що утворилися в результаті перерізу січних межами цих типових плоских перерізів зерен, розподіляють заміряні хорди у відносних частках по розмірних інтервалах у заданій розмірній шкалі, знаходять для кожного розмірного 1 UA 113112 C2 10 інтервалу середні відносні частки хорд k cp від цих типових плоских перерізів зерен і визначають коефіцієнти форми βi для кожного розмірного інтервалу шкали з відношення знайдених середніх відносних часток хорд від плоских перерізів зерен до відповідних розрахованих відносних часток хорд від кола; для урахування форми тривимірних зерен визначають коефіцієнти форми αi для чого вибирають мінімальну статистично необхідну кількість типових за формою максимальних плоских перерізів зерен, присутніх на зображенні структури, наносять на всю площину кожного з них під рівним кутом одна до другої не менше 8ми груп паралельних рівновіддалених січних, вимірюють хорди, що утворилися в результаті перерізу січних, межами цих типових максимальних плоских перерізів зерен, розподіляють заміряні хорди у частках по розмірних інтервалах у заданій розмірній шкалі, знаходять для 15 кожного розмірного інтервалу середні відносні частки хорд k cp від цих типових максимальних плоских перерізів зерен і визначають коефіцієнти форми i для кожного розмірного інтервалу шкали з відношення знайдених середніх відносних часток хорд від цих типових максимальних плоских перерізів зерен до відповідних розрахованих відносних часток діаметрів плоских перерізів (кіл) від сфери, після чого здійснюють реконструкцію розподілу Pk(d) розмірів плоских 5 20 25 30 35 40 перерізів зерен, виходячи з розподілу довжин хорд k , експериментально отриманих в результаті нанесення на зображення структури січних ліній і перерізу цих січних межами зерен структури. Недоліком даного способу є використання для знаходження розподілу плоских перерізів зерен Pk(d) вихідної інформації у вигляді розподілу хорд k ; експериментально отриманих в результаті нанесення на зображення реальної структури січних ліній і перерізу цих січних межами зерен структури, оскільки це не надає можливості створити еталони плоских перерізів тривимірних зеренних структур металевих матеріалів із заздалегідь визначеним розподілом P(Dk) розмірів тривимірних зерен. Вказаний спосіб дозволяє здійснити реконструкцію розподілу P(Dk) розмірів тривимірних зерен, виходячи з інформації про розподіл їх плоских перерізів Pk(d), але цей реконструйований розподіл характеризує конкретну зеренну структуру, яку досліджували, і розподіл розмірів його плоских перерізів не може бути еталоном із заздалегідь визначеним розподілом P(Dk). Крім того, визначення коефіцієнтів форми βi і i, згідно з цим способом, здійснюють без урахування того, що від плоского зерна k-го розмірного інтервалу отримують хорди тільки в розмірні інтервали від k-го до першого. Тому технологічні можливості застосування цього способу для створення еталонів плоских перерізів тривимірних зеренних структур металевих матеріалів з визначеним розподілом розмірів тривимірних зерен надто обмежені. В основу даного винаходу поставлена задача розробки способу створення еталонів плоских перерізів тривимірних зеренних структур металевих матеріалів з визначеним розподілом розмірів тривимірних зерен P(Dk), який дозволяє здійснити визначення коефіцієнтів форми βi і i з урахуванням того, що від плоского зерна k-го розмірного інтервалу отримують хорди тільки в розмірні інтервали від k-го до першого; вибрати як вихідну інформацію необхідний для еталона розподіл P(Dk) розмірів тривимірних зерен у заданій розмірній шкалі і здійснити реконструкцію розподілу розмірів їх плоских перерізів Pk(d) шляхом вирішення лінійних рівнянь, які встановлюють зв'язок між P(Dk) і Pk(d), після чого отримати нормовані значення Рk'(d) з 'k d k d відношення n k d k 1 ; здійснити реконструкцію розподілу розмірів хорд k шляхом вирішення лінійних рівнянь, 45 які встановлюють зв'язок між Рk'(d) і k , після чого отримати нормовані значення k ' 'k k n k k 1 відношення ; а потім за отриманим нормованим розподілом розмірів плоских перерізів зерен Рk'(d) створити еталон плоского перерізу тривимірної зеренної структури будьяким способом, в тому числі у вигляді кола із схематизованою сіткою, яка обмежує розміри зерен, або приймаючи за еталон сам розподіл розмірів плоских перерізів зерен Рk'(d); виходячи 50 з розподілів розмірів тривимірних зерен P(Dk), їх плоских перерізів Рk'(d) і розподілу хорд k ' знайти числові характеристики основних параметрів тривимірної зеренної структури, її плоского перерізу і розподілу хорд еталона із заздалегідь відомим розподілом розмірів тривимірних 2 UA 113112 C2 5 10 зерен P(Dk), що підвищує точність створеного еталона і числових характеристик його основних параметрів при одночасному забезпеченні розширення технологічних можливостей способу. Поставлена задача вирішується тим, що у способі створення еталонів плоских перерізів тривимірних зеренних структур металевих матеріалів з визначеним розподілом розмірів тривимірних зерен, який полягає в тому, що виготовляють шліф, отримують видиме зображення зеренної структури металу, для урахування форми плоских перерізів зерен визначають коефіцієнти їх форми βі, для чого обирають мінімальну статистично необхідну кількість типових за формою плоских перерізів, наносять на всю площину кожною з них під рівним кутом одна до другої не менше 8-ми груп паралельних рівновіддалених січних, вимірюють хорди, що утворилися в результаті перерізу січних, межами цих типових плоских перерізів зерен, розподіляють заміряні хорди у відносних частках по розмірних інтервалах у заданій розмірній 15 20 шкалі, знаходять для кожного розмірного інтервалу середні відносні частки хорд k cp від цих типових плоских перерізів зерен і визначають коефіцієнти форми βi для кожного розмірного інтервалу шкали з відношення знайдених середніх відносних часток хорд від плоских перерізів зерен до відповідних розрахованих відносних часток хорд від кола; для урахування форми тривимірних зерен визначають коефіцієнти форми i, для чого вибирають мінімальну статистично необхідну кількість типових за формою максимальних плоских перерізів зерен, присутніх на зображенні структури, наносять на всю площину кожного з них під рівним кутом одна до другої не менше 8-ми груп паралельних рівновіддалених січних, вимірюють хорди, що утворилися в результаті перерізу січних, межами цих типових максимальних плоских перерізів зерен, розподіляють заміряні хорди у частках по розмірних інтервалах у заданій розмірній 25 30 шкалі, знаходять для кожного розмірного інтервалу середні відносні частки хорд k cp від них типових максимальних плоских перерізів зерен і визначають коефіцієнти форми а, для кожного розмірного інтервалу шкали з відношення знайдених середніх відносних часток хорд від цих максимальних плоских перерізів зерен до відповідних розрахованих відносних часток діаметрів плоских перерізів (кіл) від сфери, здійснюють реконструкцію розподілу Pk(d) розмірів плоских перерізів зерен. При цьому, згідно з винаходом, визначення коефіцієнтів форми βi і i здійснюють з урахуванням того, що від плоского перерізу зерна k-го розмірного інтервалу отримуються хорди, тільки в розмірні інтервали від k-го до першого, а як вихідну інформацію для реконструкції розподілу Pk(d) розмірів плоских перерізів зерен вибирають необхідний для еталона розподіл P(Dk) розмірів тривимірних зерен у заданій розмірній шкалі і реконструкцію розподілу розмірів їх плоских перерізів Pk(d) здійснюють шляхом вирішення лінійних рівнянь виду: 2 2 2 2 2 2 2 2 2 2 k d a Dk Dk dk 1 b Dk 1 Dk 1 dk 1 Dk 1 dk ... f Dn Dn dk 1 Dn dk 35 40 45 , (1) де: n - кількість розмірних інтервалів у розмірній шкалі; k - порядковий номер розмірного інтервалу від 1-го до n-го; dk; dk-1 - діаметри кіл, рівновеликих плоским перерізам зерен, відповідно, k-го, (к-1)-го розмірних інтервалів; одиниці довжини; Dk; Dk+1;…; Dn - діаметри сфер, рівновеликих тривимірним зернам, відповідно, k-го, (k+1)-го, …,, n-го розмірних інтервалів; одиниці довжини; Pk(d) - відносна частка плоских перерізів зерен k-го розмірного інтервалу; P(Dk); P(Dk+1);…; P(Dn) відносні частки тривимірних зерен еталону, відповідно, k-го (k+1)-го, …, n-го розмірних інтервалів; αа; αb;…; αf- коефіцієнти форми тривимірних зерен; після чого отримують нормовані значення Pk'(d) з відношення 'k d k d n k d k 1 потім, використовуючи як вихідну інформацію отриманий нормований розподіл Pk'(d) розмірів плоских перерізів, здійснюють реконструкцію розподілу довжин хорд Рk( ) шляхом вирішення лінійних рівнянь виду: 2 2 2 k a 'k d dk 2 1 b 'k 1 d dk 1 2 1 dk 1 2 k k k 50 2 2 2 2 ... f 'n d dn k 1 dn k (2) де: n - кількість розмірних інтервалів у розмірній шкалі; k - порядковий номер розмірного інтервалу від 1-го до n-го; 3 , UA 113112 C2 k ; k 1 - довжини хорд k-го і (k-1)-го розмірних інтервалів; одиниці довжини; 5 dk; dk+1,…; dn - діаметри кіл, рівновеликих плоским перерізам зерен, відповідно, k-го, (k+1)-гo, …, n-го розмірних інтервалів; одиниці довжини; Рk( ) - відносна частка хорд k-го розмірного інтервалу; P'k(d); P'k+1(d);…; P'n(d) - відносні частки плоских перерізів зерен, відповідно, k-го, (k+1)-го, …, n-го розмірних інтервалів; βa, · βb, …,·βf - коефіцієнти форми плоских перерізів зерен; 'k 10 15 20 25 30 35 40 45 50 55 k n k k 1 після чого отримують нормовані значення k ' з відношення ; за отриманим розподілом розмірів плоских перерізів зерен P'k(d) створюють еталон плоского перерізу зеренної структури будь-яким способом, в тому числі у вигляді кола із схематизованою сіткою, яка обмежує розміри зерен, або приймаючи за еталон сам розподіл розмірів плоских перерізів зерен Pk'(d); виходячи з розподілів розмірів тривимірних зерен P(Dk), їх плоских перерізів Рk'(d) і розподілу хорд k ' знаходять числові характеристики основних параметрів тривимірної зеренної структури, її плоского перерізу і розподілу хорд еталона. Числовими характеристиками основних параметрів структури можуть бути: - розподіл розмірів тривимірних зерен P(Dk), їх плоских перерізів Рk'(d)і лінійних перерізів (хорд) k ' ; - середній, максимальний, модальний розмір сукупності зерен, їх плоских і лінійних перерізів; - кількість тривимірних зерен в одиниці об'єму, їх плоских перерізів на одиниці площини, їх лінійних перерізів на одиниці довжини; - середньоквадратичне відхилення від середнього розміру тривимірних зерен, їх плоских і лінійних перерізів; - коефіцієнт варіації розподілу тривимірних зерен, їх плоских і лінійних перерізів та ін. У пропонованому способі може застосовуватися будь-яка розмірна шкала, як рівномірна, гак і нерівномірна. Технічним результатом пропонованого способу в порівнянні з найближчим з аналогів є підвищення точності еталонів плоских перерізів тривимірних зеренних структур при одночасному забезпеченні розширення технологічних можливостей способу. Це обумовлено тим, що згідно зі способом еталон плоского перерізу зеренної структури створюють, виходячи з розподілу Рk'(d) розмірів плоских перерізів тривимірних зерен із визначеним розподілом їх розмірів P(Dk), який заздалегідь вибирають для створення еталона. Підвищення точності еталонів обумовлено також врахуванням при їх створенні форми реальних зерен, що забезпечується використанням реальних структур для визначення коефіцієнтів форми βi і i, а також урахуванням при визначенні коефіцієнтів βi і i того, що від плоского перерізу зерна k-го розмірного інтервалу отримують хорди тільки в розмірні інтервали від k-го до першого. Розширення технологічних можливостей способу забезпечується тим, що для створення еталона можна вибирати будь-який вихідний розподіл тривимірних зерен P(Dk), наприклад, одномодальний, двомодальний, багатомодальний або такий, що являє собою зерна одного конкретного розміру; а розрахувавши далі відповідний цьому заздалегідь відомому розподілу P(Dk) розподіл плоских перерізів Рk'(d), створити еталон плоских перерізів, в тому числі у вигляді кола із схематизованою сіткою, яка обмежує розміри зерен, або приймаючи за еталон сам розподіл розмірів плоских перерізів зерен Pk'(d). При цьому можна застосовувати будь-яку розмірну шкалу як рівномірну, так і нерівномірну, в тому числі таку, що застосовують у способах-аналогах, тобто у стандартах. Спосіб надає можливість визначити числові характеристики основних параметрів як тривимірної зеренної структури, так і її плоского перерізу і розподілу хорд еталона. Також розширення технологічних можливостей пропонованого способу забезпечується тим, що він може бути застосований і до створення еталонів плоских перерізів сукупностей інших елементів структури сферичної (в цьому випадку коефіцієнти форми i і βi дорівнюють одиниці), поліедричної, еліпсоїдної та подібних їм форм, в тому числі неметалевих включень, графітної і цементитної фаз, вторинних фаз, інтерметалевих фаз та ін., в цьому випадку видимим зображенням є зображення плоских перерізів цих елементів структури на шліфі. Для цих елементів структури також визначають коефіцієнти форми βi і i аналогічним пропонованому для зеренних структур способом. 4 UA 113112 C2 Розширення технологічних можливостей способу забезпечується і тим, що він дозволяє моделювати будь-які розподілення розмірів тривимірних зерен P(Dk) і встановлювати відповідні 5 10 15 20 їм розподілення плоских перерізів Pk(d) і розподілення хорд k , встановлюючи тим самим співвідношення між параметрами тривимірної структури і її плоского і лінійного перерізів. На фігурі 1 наведено приклад характерних форм плоских перерізів аустенітних зерен різного розміру (по центру кожного фото), на яких встановлювали коефіцієнти форми βi На фігурі 2 наведені напрямки (1-8) нанесення на плоский переріз аустенітного зерна 8-ми груп паралельних рівновіддалених січних і приклад нанесення січних напрямку 3 на зерно для визначення коефіцієнтів форми βi. На фігурі 3 наведено приклад характерних форм максимальних плоских перерізів зерен (по центру кожного фото), на яких встановлювали коефіцієнти форми i і βi, На фігурі 4 наведено схему еталона G6 ГОСТ 5639-82. На фігурі 5 представлено вихідний розподіл діаметрів тривимірних зерен P(Dk) () і реконструйовані за пропонованим способом розподіл діаметрів плоских перерізів цих тривимірних зерен Рk'(d) (--), за яким створюють еталон плоского перерізу зеренної структури будь-яким способом і розподіл довжин хорд k (ΔΔ) цього еталона, а також розподіл діаметрів плоских зерен еталона G6 ГОСТ 5639-82 (- -). На фігурі 6 зображено фото зеренної структури, на якій експериментально отримали розподіл довжин хорд k , який використали як вихідну інформацію для реконструкції розподілу плоских перерізів зерен Рk(d) і розподілу тривимірних зерен P(Dk) за способом найближчим з аналогів. На фігурі 7 представлено експериментально встановлений вихідний розподіл довжин хорд k (Δ- -Δ) і реконструйовані за способом найближчим з аналогів розподіли діаметрів плоских 25 30 35 перерізів зерен Рk'(d) (ο- -ο) і діаметрів тривимірних зерен Р'(Dk) (⊠ ⊠ для структури, ) зображеної на фігурі 6. Пропонований спосіб здійснюють таким чином. Зразки шліфують, полірують і піддають травленню для виявлення зеренної структури, а саме, плоского перерізу сукупності тривимірних зерен. Видиме зображення плоских перерізів зерен на шліфі фотографують або досліджують за допомогою мікроскопа або аналізаторів структури. Обробку отриманого видимого зображення плоских перерізів зерен і реконструкцію структури здійснюють, наприклад, за допомогою комп'ютера, на екран дисплея якого виводять зображення зеренної структури, і спочатку для урахування форми плоских перерізів зерен визначають коефіцієнти їх форми βi, для чого вибирають мінімальну статистично необхідну кількість типових за формою плоских перерізів (Фіг. І), наносять на всю площину кожного з них під рівним кутом одна до другої не менше 8-ми груп паралельних рівновіддалених січних (Фіг. 2), вимірюють довжини хорд , що утворилися в результаті перерізу січних межами цих типових плоских перерізів зерен, розподіляють заміряні хорди у відносних частках k по розмірних інтервалах у заданій розмірній шкалі, знаходять для кожного розмірного інтервалу середні 40 відносні частки хорд k cp від цих типових плоских перерізів зерен і визначають коефіцієнти форми βi для кожного розмірного інтервалу шкали з відношення знайдених середніх відносних часток хорд плоских перерізів зерен до відповідних розрахованих відносних часток хорд від / кола; тобто i k cp k кола , де k кола розраховують для розмірної шкали, представленої у відносному вигляді як / mах для кола діаметром d=1 умовній одиниці довжини (ум. од.) за формулою k кола 1 k 1 1 k , враховуючи при цьому, що від плоского перерізу зерна kго розмірного інтервалу отримуються хорди тільки в розмірні інтервали від k-го до першого. Далі для урахування форми тривимірних зерен визначають коефіцієнти їх форми i, для чого вибирають мінімальну статистично необхідну кількість типових за формою максимальних плоских перерізів зерен (Фіг. 3), присутніх на зображенні структури, наносять на всю площину кожного з них під рівним кутом одна до другої не менше 8-ми груп паралельних рівновіддалених січних, вимірюють довжини хорд , що утворилися в результаті перерізу січних межами цих типових максимальних плоских перерізів зерен, розподіляють заміряні хорди у відносних 2 45 50 2 частках k по розмірних інтервалах у заданій розмірній шкалі, знаходять для кожного 5 UA 113112 C2 розмірного інтервалу середні відносні частки хорд k cp від цих максимальних типових плоских перерізів зерен і визначають коефіцієнти форми i для кожного розмірного інтервалу шкали з відношення знайдених середніх відносних часток хорд від цих максимальних плоских перерізів зерен до відповідних розрахованих відносних часток діаметрів плоских перерізів від сфери, 5 k dсфери 10 / dсфери , k k cp тобто i відносному вигляді 2 1 dk 1 як d де k сфери розраховують для розмірної шкали, представленої у d/dmax для сфери діаметром D=1 ум. од. за формулою 2 1 dk , враховуючи при цьому, що від плоского перерізу зерна k-го розмірного інтервалу отримуються хорди тільки в розмірні інтервали від k-го до першого. Після цього як вихідну інформацію для реконструкції розподілу Pk(d) розмірів плоских перерізів зерен вибирають необхідний для еталона розподіл P(Dk) розмірів тривимірних зерен у заданій розмірній шкалі, а реконструкцію розподілу розмірів їх плоских перерізів Pk(d) здійснюють шляхом вирішення лінійних рівнянь виду: 2 2 2 2 2 2 2 2 2 2 k d a Dk Dk dk 1 b Dk 1 Dk 1 dk 1 Dk 1 dk ... f Dn Dn dk 1 Dn dk , 15 20 де: n - кількість розмірних інтервалів у розмірній шкалі; k - порядковий номер розмірного інтервалу від 1-го до n-го; dk; dk-1 - діаметри кіл, рівновеликих плоским перерізам зерен, відповідно, k-го, (k-1)-го розмірних інтервалів; одиниці довжини; Dk; Dk-1,·…; Dn - діаметри сфер, рівновеликих тривимірним зернам, відповідно, k-го, (k+1)-го, …, n-го розмірних інтервалів; одиниці довжини; Pk(d) - відносна частка плоских перерізів зерен k-го розмірного інтервалу; P(Dk); P(Dk+1);…; P(Dn) - відносні частки тривимірних зерен еталона, відповідно, k-го (k+1)-го, …, n-го розмірних інтервалів; αа; αb;…; αf - коефіцієнти форми тривимірних зерен; після чого отримують нормовані значення P'k(d) з відношення 'k d k d 25 n k d k 1 . Потім, використовуючи як вихідну інформацію отриманий нормований розподіл Pk'(d) розмірів плоских перерізів, здійснюють реконструкцію розподілу довжин хорд k , шляхом вирішення лінійних рівнянь виду: 2 2 2 2 2 k a 'k d dk 2 1 b 'k 1 d dk 1 2 1 dk 1 2 ... f 'n d dn 2 1 dn 2 k k k k k 30 , де: n - кількість розмірних інтервалів у розмірній шкалі; k - порядковий номер розмірного інтервалу від 7-го до п-го; k ; k 1 - довжини хорд k-го і (k-1)-го розмірних інтервалів; одиниці довжини; 35 dk; dk+1,…; dn - діаметри кіл, рівновеликих плоским перерізам зерен, відповідно, k-го, (k+1)-гo, …, n-го розмірних інтервалів; одиниці довжини; Рk( ) - відносна частка хорд k-го розмірного інтервалу; P'k(d); P'k+1(d);…; P'n(d) - відносні частки плоских перерізів зерен, відповідно, k-го, (k+1)-го, …, n-го розмірних інтервалів; βa, · βb, …,·βf - коефіцієнти форми плоских перерізів зерен; 'k 40 45 k n k k 1 після чого отримують нормовані значення k ' з відношення . За отриманим розподілом розмірів плоских перерізів зерен Рk'(d) створюють еталон плоского перерізу зеренної структури будь-яким способом, в тому числі у вигляді кола із схематизованою сіткою, яка обмежує розміри зерен, або приймаючи за еталон сам розподіл розмірів плоских перерізів зерен Pk'(d). Виходячи з розподілів розмірів тривимірних зерен P(Dk), їх плоских перерізів Рk'(d) і розподілу хорд k ' знаходять числові характеристики основних параметрів тривимірної зеренної структури, її плоского перерізу і розподілу хорд еталона. Пропонований спосіб може бути застосований і до створення еталонів плоских перерізів з іншими структурними елементами сферичної (в цьому випадку коефіцієнти форми i i βi дорівнюють одиниці), поліедричної, еліпсоїдної та подібних їм форм, в тому числі 6 UA 113112 C2 5 10 неметалевими включеннями, графітною і цементитною фазами, вторинними фазами, інтерметалевими фазами та ін., в цьому випадку видимим зображенням є зображення плоских перерізів цих елементів структури на шліфі. Для цих елементів структури теж визначають коефіцієнти форми i і βi пропонованим для зеренних структур способом. Як приклад пропонований спосіб був застосований до створення еталона зеренної структури, який би за своїми показниками відповідав еталону номера G6 за діючим стандартом ГОСТ 5639-82. Для цього спочатку проаналізували еталон номера G6 наступним чином. На основі еталона G6 в комп'ютерній програмі "Компас" створили його схему (Фіг. 4), заміряли площу кожного зерна (для цього їх пронумерували), розрахували діаметр кожного зерна, встановили, що площа максимального плоского зерна, існуючого в ньому (з урахуванням 2 збільшення зображення еталона), становить S=499,7 мкм , що визначили за допомогою програми "Компас" на комп'ютері. Виходячи з цієї площі визначили діаметр плоского зерна, як діаметр рівновеликого кола, за формулою: dS 15 20 25 30 4S 3,14 4 499,7 79,8 3,14 мкм. Тобто, встановили, що діаметр dS найбільшого зерна, яке спостерігається в еталоні G6, становить 79,8 мкм, в еталоні присутні також плоскі зерна менших розмірів. За ГОСТ 5639-82 середній діаметр плоских зерен dm визначають за формулою dm 1/ m , 2 де m - кількість плоских зерен на 1 мм площі шліфа. Для еталона G6 dm=44,2 мм. Середній діаметр сукупності плоских зерен dm, визначений як діаметр рівновеликого кола, в цьому еталоні становить 49,9 мкм, оскільки dS=1,1287dm (Даніленко Т.П. Аналіз понять величини і діаметра зерна в дослідженнях металевих структур // Металознавство та обробка металів. 2014. - № 1. - С. 45-51). Тому в подальшому визначали обидва показники розміру плоских перерізів зерен dS і dm, враховуючи, що саме dS є об'єктивною характеристикою розміру плоского перерізу тривимірного зерна. Пропонований спосіб здійснюють таким чином. Виходячи з аналізу еталона G6, який показав, що діаметр dS найбільшого зерна, яке спостерігається в еталоні G6, становить 79,8 мкм вибрали рівномірну розмірну шкалу з 10-ти інтервалів: 0; 7,98; 15,96; …; 79,8 мкм. Вихідною інформацією для створення еталона плоского перерізу тривимірної зерен мої структури металевих матеріалів з визначеним розподілом розмірів тривимірних зерен вибрали розподіл зерен P(Dk), наведений в таблиці 1. Таблиця 1 Розмірний інтервал, 6 7 мкм Межі інтервалу, мкм 39,90-47,88 47,88-55,86 Позначення P(Dk) P(D6) P(D7) Значення P(Dk), % 1 5 35 40 45 50 8 55,86-63,84 P(D8) 18 9 63,84-71,82 P(D9) 46 10 71,82-79,8 P(D10) 30 Цей розподіл вибраний таким, щоб визначений далі середній діаметр плоских перерізів сукупності тривимірних зерен відповідав рівню середнього діаметра dS і dm сукупності плоских перерізів зерен на еталоні номера G6 за діючим стандартом ГОСТ 5639-82. Далі визначили коефіцієнти форми тривимірних зерен і їх плоских перерізів. Для цього за пропонованим способом з труби розмірами 6,90,4 мм (аустенітна сталь 026 × 16Н15МЗБ) виготовили декілька металографічних шліфів, які для виявлення зеренної аустенітної мікроструктури протравили в азотній кислоті і за допомогою металографічного мікроскопу МІМ-7 отримали зображення плоских перерізів зеренної структури (Фіг. 1; 3). Визначення коефіцієнтів форми βi плоских перерізів зерен проводили для вибраної рівномірної розмірної шкали з 10-ти інтервалів з урахуванням того, що від плоского перерізу k-го розмірного інтервалу отримуються хорди тільки в розмірні інтервали від k-гo до першого, а саме: з полідисперсної системи плоских перерізів зерен тільки перерізи 10-го інтервалу, тобто найбільші за розмірами, дадуть хорди в усі 10 інтервалів (від найбільших до найменших); плоскі перерізи 9-го інтервалу дадуть хорди тільки в інтервали від 1-го до 9-го і т.д., плоскі перерізи 2го інтервалу дадуть хорди тільки в 1-й і 2-й інтервали, а перерізи 1-го інтервалу (найменші) тільки в 1-й інтервал. Для визначення коефіцієнтів форми βi проаналізували під мікроскопом форму плоских перерізів зерен, вибрали мінімальну статистично необхідну кількість типових форм різного 7 UA 113112 C2 5 розміру у 40 шт., з яких 20 шт. були максимальними плоскими перерізами, які спостерігалися на шліфі (Фіг. 3), і ще 20 зерен менших розмірів (Фіг. 1). Ці плоскі зерна сфотографували і на кожне зображення нанесли під кутом 22,5° одна до другої 8 груп паралельних січних, заміряли довжини отриманих хорд (Фіг. 2); для кожного плоского зерна встановили максимальну хорду mах і розміри усіх хорд від цього плоского зерна представили у відносному вигляді / max а потім розподілили їх у частках в рівномірній розмірній шкалі з 10-ма; 9-ма; 8-ми і т.д. інтервалами до одного інтервалу. Далі знайшли середні частки хорд розмірному інтервалу для 40-ка типових форм плоских перерізів зерен. 10 k cp пo кожному Розподіл довжин хорд від кола k кола розрахували, приймаючи діаметр кола d=1 умовній одиниці довжини (ум. од.). Рівномірна шкала з 10-ти інтервалів в умовних одиницях наступна: 0; 0,1; 0,2;…; 0,9; 1,0 ум. од. Перший розмірний інтервал включає хорди (0…0,1) ум. од., другий (0,1…0,2)ум. од. і т.д., десятий -(0,9…1,0) ум. од. Відносну кількість хорд від кола по 10-ти інтервалах розрахували за формулою: k кола 1 2 1 1 2 · k k 15 Розрахунок по інтервалах виконали наступним чином: 10 кола 1 0,9 2 0,43589 ; 9 кола 1 0,8 2 1 0,9 2 0,16411; 8 кола 1 0,7 2 1 0,8 2 0,11414 ; ……… 20 1 кола 1 0,12 0,00501. Шкала з 9-ти інтервалів в умовних одиницях така: 0; 0,111; 0,222; 0,333; 0,444; 0,556; 0,667; 0,778; 0,889; 1,0 ум. од. Відносну кількість хорд від кола по 9-ти інтервалах розрахували наступним чином: 9 кола 1 0,8892 0,45791 ; 25 8 кола 1 0,8892 1 0,7782 0,17036 ; ……. 1 кола 1 1 0,1112 0,00618. 30 Аналогічно виконали розрахунки для шкал з 8-ми, 7-ми, 6-ти, 5-ти, 4-х, 3-х, 2-х і 1-го інтервалів. Шкала з 2-х інтервалів наступна: 0; 0,5; 1,0 ум. од. і для неї відносна кількість хорд від кола розрахована наступним чином: 2 кола 1 0,5 2 0,86603; 1 кола 1 1 0,5 2 0,13397; Результати визначення k cp і k кола наведені в таблиці 2. Таблиця 2 № інтервалу, Розподіли k cp і k кола по інтервалах, % від зерен і кіл якого Показник 1 2 3 4 5 6 1 отримали хорди k cp 100 1 100 k кола 2 3 4 k cp 26,319 73,682 k кола 13,397 86,603 k cp k кола k cp 14,270 31,953 52,879 5,707 19,787 74,506 9,873 16,446 36,561 37,124 8 8 9 10 UA 113112 C2 k кола 3,175 10,222 20,459 66,144 k cp 7,444 11,028 18,669 35,895 26,952 k кола 5 2,020 6,328 11,652 20,000 60,000 k cp 5,725 8,470 12,116 20,737 32,759 20,120 k кола 6 1,404 4,303 7,690 12,097 19,178 55,327 k cp 4,823 6,855 8,835 13,221 22,497 27,147 15,134 k кола 7 1,028 3,149 5,493 8,235 12,080 18,483 51,532 k cp 3,977 5,897 6,876 9,571 13,933 22,580 25,069 12,061 k кола 8 0,784 2,391 4,122 6,100 8,540 11,919 17,731 48,412 k cp 3,311 5,194 5,727 7,384 10,355 15,065 21,317 21,832 9,573 k кола 9 0,618 1,877 3,212 4,690 6,484 8,612 11,679 17,036 45,791 k cp 2,812 4,633 5,050 5,974 7,916 10,753 16,306 19,589 19,209 7,763 k кола 10 0,501 1,519 2,586 3,742 5,049 6,603 8,586 11,414 16,411 43,589 Далі визначили коефіцієнти форми плоских перерізів зерен βi, ·для кожного розмірного інтервалу з відношення знайдених 5 k cp / до відповідних розрахованих відносних часток хорд від кола: i k cp k кола . Визначили коефіцієнти форми βk для інтервалів з 1-го по 10-й; з 1го по 9-тий; з 1-го по 8-мий; і т.д. до одного першого. Результати розрахунку коефіцієнтів форми плоских перерізів зерен наведені в таблиці 3. Таблиця 3 Коефіц. Форми плоских зерен 1-го інтервалу Коефіц. Форми плоских зерен 2-го інтервалу Коефіц. Форми плоских зерен 3-го інтервалу Коефіц. Форми плоских зерен 4-го інтервалу Коефіц. Форми плоских зерен 5-го інтервалу Коефіц, форми плоских зерен 6-го інтервалу Коефіц. β1 1,0 β2 1,965 β4 2,500 β7 3,110 β11 3,685 β16 4,078 β22 β3 0,851 β5 1,615 β8 1,609 β12 1,743 β17 1,968 β23 β6 0,710 β9 1,787 β13 1,602 β18 1,576 β24 β10 0,561 β14 1,795 Β19 1,714 β25 β15 0,449 β20 1,708 β26 9 β21 0,364 β27 β28 UA 113112 C2 Форми плоских зерен 7-го інтервалу Коефіц. Форми плоских зерен 8-го інтервалу Коефіц, форми плоских зерен 9-го інтервалу Коефіц. Форми плоских зерен 10-го інтервалу 5 10 4,692 β29 5,073 β37 5,406 β46 5,613 2,177 β30 1,608 1,605 β31 2,466 β38 β32 1,668 1,569 β39 2,767 β47 β40 1,783 1,574 β48 3,050 β49 1,953 1,596 1,862 β33 1,469 β34 1,639 β41 β35 1,894 β42 1,597 β50 0,294 1,414 β43 1,749 β51 1,568 β36 β44 1,825 β52 1,629 0,249 β45 1,282 β53 1,899 0,209 β54 1,716 β55 1,170 0,178 Для визначення коефіцієнтів форми а, тривимірних зерен проаналізували під мікроскопом форму максимальних плоских перерізів зерен, вибрали мінімальну статистично необхідну кількість типових форм у 20 шт., сфотографували їх (Фіг. 3) і на кожне зображення нанесли під ( кутом 22,5 одна до другої 8 груп паралельних січних (Фіг. 2), заміряли довжини отриманих хорд; для кожного плоского зерна встановили максимальну хорду mах і розміри усіх хорд від цього плоского зерна представили у відносному вигляді / max, потім розподілили їх у відносних частках в рівномірній розмірній шкалі з 10-ти; 9-ти; 8-ми і т.д. інтервалів і до одного інтервалу. Знайдені відносні частки хорд k , згідно з винаходом (А. с. СССР № 1397832. - Опубл. 1988 Бюл. № 19), приймали за відносні частки діаметрів плоских перерізів Рk(d) від тих тривимірних зерен, на максимальні плоскі перерізи яких були нанесені січні лінії. Після цього знайшли середні частки Рk(d)ср по кожному розмірному інтервалу для 20-ти проаналізованих типових форм плоских перерізів зерен. d 15 Розподіл діаметрів кіл від сфери k сфери дорівнює розподілу довжин хорд від кола k кола (Даніленко Т.П. Визначення параметрів об'ємної зеренної структури металевих матеріалів / / Металознавство та обробка металів. - 2013. -№ 3. С. 35-42), тому розрахований розподіл k кола використали для визначення як коефіцієнтів β , так і коефіцієнтів . i i Результати визначення k cp і k кола наведені в таблиці 4. Таблиця 4, № інтервалу, від зерен і кіл якого зник отримують хорди 1 2 3 4 Розподіли k cp 1 k cp 3 4 100 k кола і k кола інтервалах, % 100 k cp 25,428 74,573 k кола 13,397 86,603 k cp 14,095 29,627 54,497 k кола 5,707 19,787 74,506 k cp 10,275 15,153 34,641 39,932 k кола 3,175 10,222 20,459 66,144 10 5 6 7 8 9 10 UA 113112 C2 k cp 5 8,029 10,056 17,821 34,802 29,266 k кола 2,020 6,328 11,652 20,000 60,000 k cp 6 6,336 7,609 11,467 19,960 32,427 22,051 k кола 1,404 4,303 7,690 12,097 19,178 55,327 k cp 7 5,507 6,367 8,239 12,508 21,193 28,793 17,091 k кола 1,028 3,149 5,493 8,235 12,080 18,483 51,532 k cp 8 4,570 5,705 6,207 8,947 13,403 21,238 25,887 14,061 k кола 0,784 2,391 4,122 6,100 8,540 11,919 17,731 48,412 k cp 9 3,884 5,143 5,051 7,012 9,628 14,574 20,290 22,401 11,472 k кола 0,618 1,877 3,212 4,690 6,484 8,612 11,679 17,036 45,791 k cp 10 3,403 4,626 4,499 5,547 7,481 10,339 15,625 19,176 19,882 9,422 k кола 0,501 1,519 2,586 3,742 5,049 6,603 8,586 11,414 16,411 43,589 Визначали коефіцієнти форми i для інтервалів з 1-го по 10-й; з 1-го по 9-тий; з 1-го по 8мий; і т.д. до одного першого. Результати розрахунку коефіцієнтів форми тривимірних зерен i наведені в таблиці 5. 5 Таблиця 5 Коефіцієнт форми зерен 1-го інтервалу Коефіцієнті форми зерен 2-го інтервалу Коефіцієнті форми зерен 3-го інтервалу Коефіцієнті форми зерен 4-го інтервалу Коефіцієнті форми зерен 5-го інтервалу Коефіцієнті форми зерен 6-го інтервалу Коефіцієнті форми зерен 7-го інтервалу Коефіцієнті форми зерен 8-го інтервалу Коефіцієнті форми зерен 9-го α1 1,0 α2 1,898 α4 2,470 α7 3,236 α11 3,975 α16 4,513 α22 5,357 α29 5,829 α37 6,285 α3 0,861 α5 1,497 α8 1,482 α12 1,589 α17 1,768 α23 2,022 α30 2,386 α38 2,740 α6 0,731 α9 1,693 α13 1,529 α18 1,491 α24 1,500 α31 1,506 α39 1,573 α10 0,604 α14 1,740 α19 1,650 α25 1,519 α32 1,467 α40 1,495 α15 0,488 α20 1,691 α26 1,779 α33 1,569 α41 1,485 11 α21 0,399 α27 1,558 α34 1,782 α42 1,692 α28 0,332 α35 1,46 α43 1,737 α36 0,29 α44 1,315 α45 0,251 UA 113112 C2 інтервалу Коефіцієнті α46 форми зерен 10-го 6,792 інтервалу α47 3,045 α48 1,740 α49 1,482 α50 1,482 α51 1,566 α52 α53 1,820 1,680 α54 1,212 α55 0,216 Далі для розрахунку часток Pk(d) склали рівняння виду (1): 2 2 10 d 55 D10 D10 d9 ; 2 2 2 2 2 2 9 d 45 D9 D9 d8 54 D10 D10 d8 D10 d9 ; 5 2 2 2 2 2 2 2 2 2 2 8 d 36 D8 D8 d7 44 D9 D9 d7 D9 d8 53 D10 D10 d7 D10 d8 ; 2 2 2 2 2 2 2 7 d 28 D7 D7 d2 35 D8 D8 d2 D8 d7 43 D9 D9 d2 D9 d7 6 6 6 2 2 2 2 52 D10 D10 d6 D10 d7 ; 2 2 2 2 2 2 2 6 d 21D6 D2 d5 27 D7 D7 d5 D7 d2 34 D8 D8 d5 D8 d2 6 6 6 2 2 2 2 2 2 42 D9 D9 d5 D9 d2 51D10 D10 d5 D10 d2 ; 6 6 2 2 2 2 2 2 2 2 2 2 2 5 d 20 D6 D6 d4 D6 d5 26 D7 D7 d4 D7 d5 33 D8 D8 d2 D8 d5 4 2 2 2 2 2 2 41D9 D9 d2 D9 d5 50 D10 D10 d2 D10 d5 ; 4 4 10 2 2 2 2 4 d 19 D6 D2 d3 D2 d2 25 D7 D7 d3 D7 d2 6 6 4 4 2 2 2 2 2 2 40 D9 D9 d3 D9 d2 49 D10 D10 d3 D10 d2 ; 4 4 2 2 2 2 32 D8 D8 d3 D8 d4 2 2 2 2 2 2 2 3 d 18 D6 D2 d2 D2 d3 24 D7 D7 d2 D7 d3 31D8 D8 d2 D8 d3 6 2 6 2 2 2 2 2 2 2 2 39 D9 D9 d2 D9 d3 48 D10 D10 d2 D10 d3 ; 2 2 2 2 2 2 2 2 2 2 d 17 6 D D2 d1 D2 d2 23 7 D D7 d1 D7 d2 30 8 D D8 d1 D8 d2 6 6 2 2 2 2 2 2 2 2 2 2 2 38 9 D D9 d1 D9 d2 47 10 D D10 d1 D10 d2 ; 15 2 2 2 2 2 2 2 2 2 2 1d 16 6 D D2 d0 D2 d1 22 7 D D7 d0 D7 d1 29 8 D D8 d0 D8 d1 6 6 2 2 2 2 2 2 2 2 37 9 D D9 d0 D9 d1 46 10 D D10 d0 D10 d1 . Після підстановки числових значень в рівняння виконали розрахунки: 10 d 0,21 0,30 79,8 2 71822 2,2540041 , 20 9 d 0,251 0,46 71822 63,842 1,212 0,30 79,8 2 63,842 79,8 2 71822 8,5606098 , , 8 d 0,29 0,18 63,842 55,862 1315 0,46 71822 55,862 71822 63,842 , , , 2 2 2 2 168 0,30 79,8 55,86 79,8 63,8 13,6076093 , 12 UA 113112 C2 7 d 0,332 0,05 55,862 47,882 1 46 0,18 63,842 47,882 63,842 55,862 , 2 2 2 2 2 2 1737 0,46 7182 47,88 7182 55,86 182 0,30 79,8 47,88 79,8 2 55,862 13,8969188 , , , , 2 2 2 2 2 2 6 d 0,399 0,01 47,88 39,9 1,558 0,05 55,86 39,9 55,86 47,88 1782 0,18 63,842 39,9 2 63,842 47,882 1 692 0,46 71822 39,9 2 71822 47,882 , , , , 2 2 2 2 1566 0,30 79,8 39,9 79,8 47,88 10,6397833 , 5 d 1 691 0,01 47,882 31922 47,882 39,9 2 1779 0,05 55,862 31922 55,862 39,9 2 , , , , 1569 0,18 63,842 31922 63,842 39,9 2 1 485 0,46 71822 31922 71822 39,9 2 , , , , , , 2 2 2 2 1 482 0,30 79,8 3192 79,8 39,9 7,2431144 , , 4 d 1 650 0,01 47,882 23,942 47,882 31922 1519 0,05 55,862 23,942 55,862 31922 , , , , 2 2 2 2 2 2 2 2 1,467 0,18 63,84 23,94 63,84 3192 1 495 0,46 7182 23,94 7182 3192 , , , , , 2 2 2 2 1,482 0,30 79,8 23,94 79,8 3192 5,1244166 , 5 3 d 1 491 0,01 47,882 15,962 47,882 23,942 1500 0,05 55,862 15,962 55,862 23,942 , , 1,506 0,18 63,842 15,962 63,842 23,942 1,573 0,46 71822 15,962 71822 23,942 , , 1,740 0,30 79,8 2 15,962 79,8 2 23,942 3,7475442 2 d 1768 0,01 47,882 7,982 47,882 15,962 2,022 0,05 55,862 7,982 55,862 15,962 , 2,386 0,18 63,842 7,982 63,842 15,962 2,740 0,46 71822 7,982 71822 15,962 , , 3,045 0,30 79,8 2 7,982 79,8 2 15,962 3,679969 1d 4,513 0,01 47,88 47,882 7,982 5,357 0,05 55,86 55,862 7,982 2 2 2 2 5,829 0,18 63,84 63,84 7,98 6,285 0,46 7182 7182 7,98 , , 6,792 0,30 79,8 79,8 2 7,982 2,8097897 Вирішили рівняння, наприклад, за допомогою комп'ютера, в результаті чого знайшли всі значення Pk(d), після чого отримали нормовані значення Рk'(d) із співвідношення 'k d k d 10 15 n k d k 1 , які у сукупності являють собою розподіл діаметрів плоских перерізів зерен для створення еталона структури. Отримані результати наведені в таблиці 6. Оскільки однією з характеристик номера зерна за ГОСТ 5639-82 є також середній умовний діаметр зерна dL, який по суті є середньою довжиною хорд, отриманих в результаті нанесення на зображення структури січних ліній і перерізу цих ліній межами зерен, то для визначення dL еталона, який створювали, здійснили реконструкцію розподілу хорд k еталона. Таблиця 6 №№ інтервалів k 1 2 3 4 5 6 Межі інтервалів min max мкм 0-7,98 7,98-15,96 15,96-23,94 23,94-31,92 31,92-39,9 39,9-47,88 Розподіл діаметрів плоских Розраховані відносні частки перерізів зерен (нормовані Рk(d) відносні частки) Pk’(d) 2,8097897 0,03922627 3,6799690 0,0514222 3,7475442 0,0523665 5,1244166 0,0716063 7,2431144 0,1012120 10,6397833 0,1486756 13 UA 113112 C2 7 8 9 10 47,88-55,86 55,86-63,84 63,84-71,82 71,82-79,8 13,8969188 13,6076093 8,5606098 2,2540041 0,1941893 0,1901467 0,1196221 0,0314964 Для цієї реконструкції склали наступні рівняння виду (2): 2 10 55 '10 d d10 2 ; 9 2 2 2 9 45 '9 d d9 2 54 '10 d d10 2 d10 2 8 8 9 5 10 2 2 2 8 36 '8 d d8 2 44 '9 d d9 2 d9 2 7 7 8 ; ; 2 2 2 2 53 '10 d d10 7 d10 8 ; 2 2 2 2 2 7 28 '7 d d7 2 35 '8 d d8 2 d8 2 43 '9 d d9 2 d9 2 6 6 7 6 7 2 2 2 2 52 '10 d d10 6 d10 7 ; 2 2 2 2 6 21' 6 d d2 2 27 '7 d d7 2 d7 2 34 '8 d d8 2 d8 2 6 5 5 6 5 6 2 2 2 2 2 2 2 2 42 '9 d d9 5 d9 6 51'10 d d10 5 d10 6 ; 2 2 2 5 15 '5 d d5 2 20 ' 6 d d2 2 d2 2 26 '7 d d7 2 d7 2 4 6 4 6 5 4 5 2 2 2 2 2 2 2 2 2 2 2 33 '8 d d8 4 d8 5 41'9 d d9 4 d9 5 50 '10 d d10 4 d10 2 ; 5 2 2 4 10 ' 4 d d2 2 14 '5 d d5 2 d5 2 19 ' 6 d d2 2 d2 2 4 3 3 4 6 3 6 4 2 2 2 2 2 2 2 2 2 2 2 25 '7 d d7 3 d7 4 32 '8 d d8 3 d8 4 40 '9 d d9 3 d9 2 4 2 2 49 '10 d d10 2 d10 2 ; 3 4 2 2 2 2 2 3 6 '3 d d3 2 9 ' 4 d d4 2 d2 2 13 '5 d d5 2 d5 2 2 4 3 2 3 2 2 2 2 18 ' 6 d d2 2 d2 2 24 '7 d d7 2 d7 2 31'8 d d8 2 d8 2 6 2 6 3 2 3 2 3 2 2 2 2 2 2 2 2 39 '9 d d9 2 d9 3 48 '10 d d10 2 d10 3 ; 2 2 2 2 2 2 3 ' 2 d d2 1 5 '3 d d3 1 d3 2 8 ' 4 d d2 1 d2 2 2 2 4 4 2 2 2 2 2 2 2 2 2 2 2 2 12 '5 d d5 1 d5 2 17 ' 6 d d6 1 d6 2 23 '7 d d7 1 d7 2 2 2 2 2 2 2 2 2 2 2 30 '8 d d8 1 d8 2 38 '9 d d9 1 d9 2 47 '10 d d10 1 d10 2 ; 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1'1 d d1 0 2 ' 2 d d2 0 d2 1 4 '3 d d3 0 d3 1 2 2 2 2 2 7 ' 4 d d2 2 d2 1 11'5 d d5 2 d5 1 16 ' 6 d d2 2 d2 1 4 0 4 0 6 0 6 2 2 2 2 2 2 2 2 2 2 2 2 22 '7 d d7 0 d7 1 29 '8 d d8 0 d8 1 37 '9 d d9 0 d9 1 2 2 2 46 '10 d d10 2 d10 1 ; 0 Після підстановки числових значень вирішили рівняння, використовуючи як вихідну інформацію знайдені нормовані частки P'k(d) 15 10 0,178 0,0314964 79,8 2 71822 0,195012 , 9 0,209 0,1196221 71822 63,842 1170 0,0314964 79,8 2 63,842 79,8 2 71822 1,3051915; , , , 14 UA 113112 C2 8 0,249 0,1901467 63,842 55,862 1282 0,1196221 71822 55,862 71822 63,842 , , , 1716 0,0314964 79,8 2 55,862 79,8 2 63,8 2 3,8325785; , 7 0,294 0,1941893 55,862 47,882 1 414 0,1901467 63,842 47,882 63,842 55,862 , 1 825 0,1196221 71822 47,882 71822 55,862 1 899 0,0314964 79,8 2 47,882 79,8 2 55,862 , , , , 6,9275474; 6 0,364 0,1486756 47,882 39,9 2 1,469 0,1941893 55,862 39,9 2 55,862 47,882 1,894 0,1901467 63,842 39,9 2 63,842 47,882 1,749 0,1196221 71822 39,9 2 71822 47,882 , , 1,629 0,0314964 79,8 2 39,9 2 79,8 2 47,882 8,6813726; 5 0,449 0,101212 39,9 2 31922 1,708 0,1486756 47,88 2 31922 47,88 2 39,9 2 , , 2 2 2 2 2 2 1,862 0,1941893 55,86 3192 55,86 39,9 1,639 0,1901467 63,84 3192 63,84 2 39,9 2 , , 1,597 1,1196221 71822 31922 71822 39,9 2 1,568 0,0314964 79,8 2 31922 79,8 2 39,9 2 8,6500217; , , , , 4 0,561 0,0716063 31922 23,94 2 1,795 0,101212 39,9 2 23,942 39,9 2 31922 , , 1,714 0,1486756 47,88 2 23,942 47,88 2 31922 1,605 0,1941893 55,86 2 23,942 55,862 31922 , , 5 1,569 0,1901467 63,842 23,94 2 63,842 31922 1,574 0,1196221 71822 23,942 71822 31922 , , , , 1,596 0,0314964 79,8 2 23,942 79,8 2 31922 7,1602802; , 3 0,710 0,0523665 23,942 15,962 1787 0,0716063 31922 15,962 31922 23,942 , , , 1 602 0,101212 39,9 2 15,962 39,9 2 23,942 1576 0,1486756 47,882 15,962 47,882 23,942 , , 1 608 0,1941893 55,862 15,962 55,862 23,942 1 668 0,1901467 63,842 15,962 63,842 23,942 , , 1783 0,1196221 71822 15,962 71822 23,942 1953 0,0314964 79,8 2 15,962 79,8 2 23,942 , , , , 5,5248747; 2 0,851 0,051422 15,962 7,982 1,615 0,0523665 23,942 7,982 23,942 15,962 2 2 2 2 2 2 1,609 0,0716063 3192 7,98 3192 15,96 1,743 0,101212 39,9 7,98 39,9 2 15,962 , , 2 2 2 2 2 2 2 1,968 0,1486756 47,88 7,98 47,88 15,96 2,177 0,1941893 55,86 7,98 55,86 15,962 2 2 2 2 2 2 2 2 2,466 0,1901467 63,84 7,98 63,84 15,96 2,767 0,1196221 7182 7,98 7182 15,96 , , 3,050 0,0314964 79,8 2 7,982 79,8 2 15,962 4,4528371; 1 1 0,0392627 7,98 1965 0,051422215,96 15,962 7,982 , 2,500 0,0523665 23,94 23,942 7,982 3,110 0,0716063 3192 31922 7,982 , , 3,685 0,101212 39,9 39,9 2 7,982 4,078 0,1486756 47,88 47,882 7,982 4,692 0,1941893 55,86 55,862 7,982 5,073 0,1901467 63,84 63,842 7,982 2 2 2 2 5,406 0,1196221 7182 7182 7,98 5,613 0,0314964 79,8 79,8 7,98 3,0043542; , , Вирішили рівняння, наприклад, за допомогою комп'ютера, в результаті чого знайшли всі 10 значення 'k k k , після чого отримали нормовані значення k ' із співвідношення n k k 1 . Розраховані за пропонованим способом розподіли діаметрів плоских перерізів зерен P'k(d) і 15 хорд k ' , а також вихідний розподіл діаметрів тривимірних зерен P(Dk) представлені графічно (Фіг. 5). На Фіг. 5 представлено також розподіл діаметрів плоских зерен еталона G6 ГОСТ 563982, встановлений шляхом вимірювання площі кожного плоского зерна на схемі еталона за допомогою комп'ютерної програми "Компас", наступного визначення діаметра ds кожного зерна і встановлення розподілу цих діаметрів Pk(d) за розмірами у вибраній шкалі. 15 UA 113112 C2 Отримані результати наведені в таблиці 7. Таблиця 7 №№ інтервалів k 1 2 3 4 5 6 7 8 9 10 5 Межі інтервалів min max мкм Розраховані відносні частки k 0-7,98 7,98-15,96 15,96-23,94 23,94-31,92 31,92-39,9 39,9-47,88 47,88-55,86 55,86-63,84 63,84-71,82 71,82-79,8 3,0043542 4,4528371 5,5248747 7,1602802 8,6500217 8,6813726 6,9275474 3,8325785 1,3051915 0,1950120 Розподіл діаметрів плоских перерізів зерен (нормовані відносні частки) 'k 0,0604084 0,0895329 0,1110379 0,1439059 0,1738465 0,1744765 0,1392285 0,0770264 0,0262315 0,0039193 На заключному етапі виконали розрахунок усіх параметрів для сукупностей тривимірних зерен, їх плоских і лінійних перерізів еталона. Усі результати представлені в таблиці 8. Таблиця 8 Об'єкт аналізу Значення параметрів 71,74 7,00 9,76 71,82 79,8 5173 Параметри структури Середній діаметр тривимірних зерен Dcp, мкм Середньоквадратичне відхилення від середнього діаметра, мкм Розподіл зерен Коефіцієнт варіації розподілу діаметрів зерен в об'ємі, % в об'ємі P(Dk) Модальний діаметр зерен, мкм Максимальний діаметр зерен, мкм 3 Кількість зерен в 1 мм , шт. Середній діаметр плоских перерізів зерен dm за ГОСТ 563982,мкм Середній діаметр плоских перерізів зерен dS, мкм Розподіл Середиьоквадратичне відхилення від середнього діаметра, мкм плоских перерізів зерен Коефіцієнт варіації розподілу діаметрів плоских перерізів зерен, Pk(d) % Модальний розмір діаметрів плоских перерізів, мкм 2 Кількість плоских перерізів зерен m на 1 мм , шт. Середній розмір хорд (за ГОСТ dL), мкм Середньоквадратичне відхилення від середнього розміру хорд, Розподіл хорд мкм Коефіцієнт варіації розподілу розмірів хорд, % k Модальний розмір хорд, мкм Кількість хорд на 1 мм, шт. Номер зерна за стандартом ГОСТ 5639-82 G6 10 15 20 44,2 49,92 18,08 36,22 55,86 511 39,36 16,55 42,04 47,88 25 За основними параметрами (m; dm; dL) еталон, створений за пропонованим способом у вигляді розподілу діаметрів плоских перерізів зерен, відповідає номеру зерна G6 і при цьому відомо, який розподіл розмірів тривимірних зерен P(Dk) (див. табл. 1) дає па металографічному шліфі плоский переріз з такими параметрами (див. табл. 8). Порівняння параметрів тривимірної структури і її плоского перерізу показав, що середній діаметр Dcp сукупності тривимірних зерен в 1,44 разу більший за середній діаметр dS сукупності їх плоских перерізів, а за коефіцієнтом варіації, який є показником різнозернистості структури, тривимірна структура значно однорідніша (у 3,7 разу), ніж та, що спостерігається на її плоскому перерізі. Визначений за пропонованим способом розподіл діаметрів плоских перерізів зерен P'k(d) є основою для створення еталона структури будь-яким способом, в тому числі у вигляді кола із схематизованою сіткою, яка обмежує розміри зерен, як це застосовано в стандартах ГОСТ 5639-82 і ISO 643:2012, або приймаючи за еталон сам розподіл розмірів плоских перерізів зерен. 16 UA 113112 C2 Використання способу найближчого з аналогів, в якому як вихідну інформацію для знаходження розподілу плоских перерізів зерен Pk(d) застосували експериментально отриманий 5 10 15 20 25 30 35 40 45 50 55 розподіл довжин хорд k , визначений на структурі, наведеній на Фіг. 6, в результаті нанесення на зображення структури січних ліній і перерізу цих січних межами зерен структури показало наступне. За середнім умовним діаметром зерна dL=50,71 мкм величину зерна наведеної структури визначили як таку, що займає положення між номерами G6 і G5. При цьому максимальний діаметр плоских перерізів зерен, що спостерігалися на структурі дорівнював 156 мкм. Виконали реконструкцію розподілу Pk(d) розмірів плоских перерізів зерен, виходячи з розподілу довжин експериментально отриманих хорд k , а потім - реконструкцію розподілу розмірів тривимірних зерен P(Dk), виходячи з реконструйованого розподілу Pk(d). Отримані розподіли k , Pk(d), P(Dk) Для цієї структури наведені на Фіг. 7. Середній діаметр плоских перерізів зерен реконструйованої структури становив dm=50,30 мкм, що займає положення між номерами G6 і G5 за ГОСТ 5639-82; середній діаметр зерен реконструйованої тривимірної структури становив Dcp=71,41 мкм. Реконструйований розподіл Pk(d), який характеризував конкретну зеренну структуру, яку досліджували, не надав можливості створити еталон плоских перерізів тривимірної зеренної структури металевих матеріалів із заздалегідь визначеним розподілом розмірів тривимірних зерен P(Dk), оскільки розподіл P(Dk) не був заздалегідь визначеним, а був реконструйованим. Точність пропонованого способу створення еталонів плоских перерізів тривимірних зеренних структур металевих матеріалів з визначеним розподілом розмірів тривимірних зерен в порівнянні з найближчим з аналогів підвищилася в декілька разів, оскільки згідно зі способом еталон у вигляді розподілу розмірів плоских перерізів зерен P'k(d) був отриманий, виходячи з розподілу тривимірних зерен P(Dk), який заздалегідь вибрали для створення еталона і який характеризував тривимірну зеренну структуру, що впливає на властивості металевих виробів. Підвищення точності еталонів обумовлено також врахуванням при їх створенні форми реальних зерен, що забезпечується використанням реальних структур для визначення коефіцієнтів форми зерен і їх плоских перерізів і урахуванням при їх визначенні того, що від плоского зерна к-то розмірного інтервалу отримують хорди тільки в розмірні інтервали від k-го до першого. Розширення технологічних можливостей способу забезпечується тим, що для створення еталона можна вибирати будь-який вихідний розподіл тривимірних зерен P(Dk), наприклад, одномодальний, двомодальний, багатомодальний або такий, що являє собою зерна одного конкретного розміру; а розрахувавши далі відповідний цьому заздалегідь відомому розподілу P(Dk) розподіл плоских перерізів P'k(d), створити еталон будь-яким способом, в тому числі у вигляді кола із схематизованою сіткою, яка обмежує розміри зерен, або приймаючи за еталон сам розподіл розмірів плоских перерізів зерен P'k(d). При цьому можна застосовувати будь-яку розмірну шкалу як рівномірну, так і нерівномірну, в тому числі таку, яку застосовують у способах-аналогах. Спосіб надає можливість визначити числові характеристики основних параметрів як тривимірної зеренної структури, так і її плоского перерізу і розподілу хорд еталона. Крім того, значне розширення технологічних можливостей пропонованого способу обумовлене й тим, що він може бути застосований і до створення еталонів структури із складовими сферичної форми (в цьому випадку коефіцієнти форми i і βi дорівнюють одиниці), а також елементів структури поліедричної, еліпсоїдної та подібних їм форм, в тому числі неметалевих включень, графітної і цементної фаз, вторинних фаз, інтерметалевих фаз та ін., в цьому випадку видимим зображенням структури для визначення коефіцієнтів форми i і βi є зображення плоских перерізів цих елементів структури на шліфі. Розширення технологічних можливостей пропонованого способу обумовлене також тим, що з метою моделювання співвідношення розподілів розмірів тривимірних зерен P(Dk) і встановлення відповідних їм розподілів плоских перерізів Pk(d) і розподілів хорд k можливо вибрати будь-який розподіл розмірів тривимірних зерен P(Dk), що дозволяє точніше встановлювати ці співвідношення. Таким чином застосування пропонованого способу в порівнянні з найближчим з аналогів дозволяє підвищити точність при одночасному розширенні технологічних можливостей способу створення еталонів плоских перерізів тривимірних зеренних структур металевих матеріалів з визначеним розподілом розмірів тривимірних зерен, що збільшує коло його практичного застосування, наприклад, при вивченні впливу параметрів структури на властивості цих матеріалів, при розробці технологічних процесів виготовлення металевих виробів, способів і режимів їх термічної обробки, при стереологічних дослідженнях структури. 17 UA 113112 C2 ФОРМУЛА ВИНАХОДУ 5 10 15 20 25 30 1. Спосіб створення еталонів плоских перерізів тривимірних зеренних структур металевих матеріалів з визначеним розподілом розмірів тривимірних зерен, який полягає в тому, що виготовляють шліф, отримують видиме зображення зеренної структури металу, для урахування форми плоских перерізів зерен визначають коефіцієнти їх форми i, для чого вибирають мінімальну статистично необхідну кількість типових за формою плоских перерізів, наносять на всю площину кожного з них під рівним кутом одна до другої не менше 8-ми груп паралельних рівновіддалених січних, вимірюють хорди, що утворилися в результаті перерізу січних межами цих типових плоских перерізів зерен, розподіляють заміряні хорди у відносних частках по розмірних інтервалах у заданій розмірній шкалі, знаходять для кожного розмірного інтервалу середні відносні частки хорд Рk( )ср від цих типових плоских перерізів зерен і визначають коефіцієнти форми i для кожного розмірного інтервалу шкали з відношення знайдених середніх відносних часток хорд від плоских перерізів зерен до відповідних розрахованих відносних часток хорд від кола; для урахування форми тривимірних зерен визначають коефіцієнти форми i, для чого вибирають мінімальну статистично необхідну кількість типових за формою максимальних плоских перерізів зерен, присутніх на зображенні структури, наносять на всю площину кожного з них під рівним кутом одна до другої не менше 8-ми груп паралельних рівновіддалених січних, вимірюють хорди, що утворилися в результаті перерізу січних межами цих типових максимальних плоских перерізів зерен, розподіляють заміряні хорди у частках по розмірних інтервалах у заданій розмірній шкалі, знаходять для кожного розмірного інтервалу середні відносні частки хорд Рk( )ср від цих типових максимальних плоских перерізів зерен і визначають коефіцієнти форми i для кожного розмірного інтервалу шкали з відношення знайдених середніх відносних часток хорд від цих типових максимальних плоских перерізів зерен до відповідних розрахованих відносних часток діаметрів плоских перерізів (кіл) від сфери, після чого здійснюють реконструкцію розподілу Pk(d) розмірів плоских перерізів зерен, який відрізняється тим, що визначення коефіцієнтів форми i і i здійснюють з урахуванням того, що від плоского перерізу зерна k-го розмірного інтервалу отримуються хорди тільки в розмірні інтервали від k-го до першого; а як вихідну інформацію для реконструкції розподілу Pk(d) розмірів плоских перерізів зерен вибирають необхідний для еталона розподіл P(Dk) розмірів тривимірних об'ємних зерен у заданій розмірній шкалі і реконструкцію розподілу розмірів їх плоских перерізів Pk(d) здійснюють шляхом вирішення лінійних рівнянь виду: 2 2 2 2 2 2 2 2 2 2 Pk d aPDk Dk dk 1 bPDk 1 Dk 1 dk 1 Dk 1 dk ... f PDn Dn dk 1 Dn dk , 35 40 45 де: n - кількість розмірних інтервалів у розмірній шкалі; k - порядковий номер розмірного інтервалу від 1-го до n-го; dk; dk-1 - діаметри кіл, рівновеликих плоским перерізам зерен, відповідно, k-го, (k-1)-го розмірних інтервалів; одиниці довжини; Dk; Dk+1;..., Dn - діаметри сфер, рівновеликих тривимірним зернам, відповідно, k-го, (k+1)-го,..., nго розмірних інтервалів; одиниці довжини; Pk(d) - відносна частка плоских перерізів зерен k-го розмірного інтервалу; P(Dk); P(Dk+1);...; P(Dn) відносні частки тривимірних зерен еталона, відповідно, k-го, (k+1)-го,..., nго розмірних інтервалів; a; b;...; f - коефіцієнти форми тривимірних зерен; після чого отримують нормовані значення Pk'(d) з відношення 'k d k d k d n ; потім, використовуючи як вихідну інформацію, отриманий k 1 нормований розподіл Pk'(d) розмірів плоских перерізів здійснюють реконструкцію розподілу довжин хорд Рk( ) шляхом вирішення лінійних рівнянь виду: 2 2 2 2 2 Pk aP'k d dk 2 1 bP'k 1 d dk 1 2 1 dk 1 2 ... f P'n d dn 2 1 dn 2 , де: n k k k k k 50 кількість розмірних інтервалів у розмірній шкалі; k - порядковий номер розмірного інтервалу від 1-го до n-го; k ; k 1 - довжини хорд k-го і (k-1)-го розмірних інтервалів; одиниці довжини; dk; dk+1;...; dn - діаметри кіл, рівновеликих плоским перерізам зерен, відповідно, k-гo, (k+1)-го,..., n-го розмірних інтервалів; одиниці довжини; Рk( ) - відносна частка хорд k-го розмірного інтервалу; 18 UA 113112 C2 P'k(d); P'k+1(d);...; P'n(d) - нормовані відносні частки плоских перерізів зерен, відповідно, k-го, (k+1)-го,..., n-го розмірних інтервалів; a; b;...; βf - коефіцієнти форми плоских перерізів зерен; після чого отримують нормовані значення Рk( ) з відношення P'k Pk Pk n ; k 1 5 10 15 20 за отриманим розподілом розмірів плоских перерізів зерен Pk'(d) створюють еталон плоского перерізу зеренної структури у вигляді кола із схематизованою сіткою, яка обмежує розміри зерен, або приймаючи за еталон сам розподіл розмірів плоских перерізів зерен Pk'(d); виходячи з розподілів розмірів тривимірних зерен P(Dk), їх плоских перерізів Pk'(d) і розподілу хорд Рk'( ) знаходять числові характеристики основних параметрів тривимірної зеренної структури, її плоского перерізу і розподілу хорд. 2. Спосіб за п. 1, який відрізняється тим, що видимим зображенням структури може бути зображення плоских перерізів будь-яких елементів структури сферичної (в цьому випадку коефіцієнти форми i і βi дорівнюють одиниці), поліедричної, еліпсоїдної та подібних їм форм, в тому числі неметалевих включень, графітної і цементитної фаз, вторинних фаз, інтерметалевих фаз та ін., для яких знаходять відповідні коефіцієнти форми їх плоских перерізів βі і коефіцієнти форми самих тривимірних елементів структури i і створюють еталони плоских перерізів цих структур. 3. Спосіб за п. 1, який відрізняється тим, що для моделювання співвідношення розподілів розмірів тривимірних зерен P(Dk) і встановлення відповідних їм розподілів плоских перерізів Pk'(d) і розподілів хорд Рk'( ) вибирають будь-який розподіл розмірів тривимірних зерен P(Dk). 19 UA 113112 C2 20 UA 113112 C2 21 UA 113112 C2 Комп’ютерна верстка І. Скворцова Державна служба інтелектуальної власності України, вул. Василя Липківського, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут інтелектуальної власності”, вул. Глазунова, 1, м. Київ – 42, 01601 22
ДивитисяДодаткова інформація
МПК / Мітки
МПК: G01N 33/20, G01N 21/00, G01N 21/29
Мітки: розподілом, матеріалів, перерізів, розмірів, визначеним, зерен, плоских, створення, зеренних, тривимірних, структур, металевих, еталонів, спосіб
Код посилання
<a href="https://ua.patents.su/24-113112-sposib-stvorennya-etaloniv-ploskikh-pereriziv-trivimirnikh-zerennikh-struktur-metalevikh-materialiv-z-viznachenim-rozpodilom-rozmiriv-trivimirnikh-zeren.html" target="_blank" rel="follow" title="База патентів України">Спосіб створення еталонів плоских перерізів тривимірних зеренних структур металевих матеріалів з визначеним розподілом розмірів тривимірних зерен</a>
Попередній патент: Біорозкладальне паковання для харчових продуктів
Наступний патент: Протитечійний шнековий екстрактор безперервної дії з проміжним віджимом рослинної сировини
Випадковий патент: Пристрій охолодження, порувата охолоджувальна вставка, спосіб охолодження, вилитий пластмасовий виріб, охолоджувальна труба та спосіб формування охолоджувальної труби