Спосіб визначення теплового опору кристала субмікронного транзистора

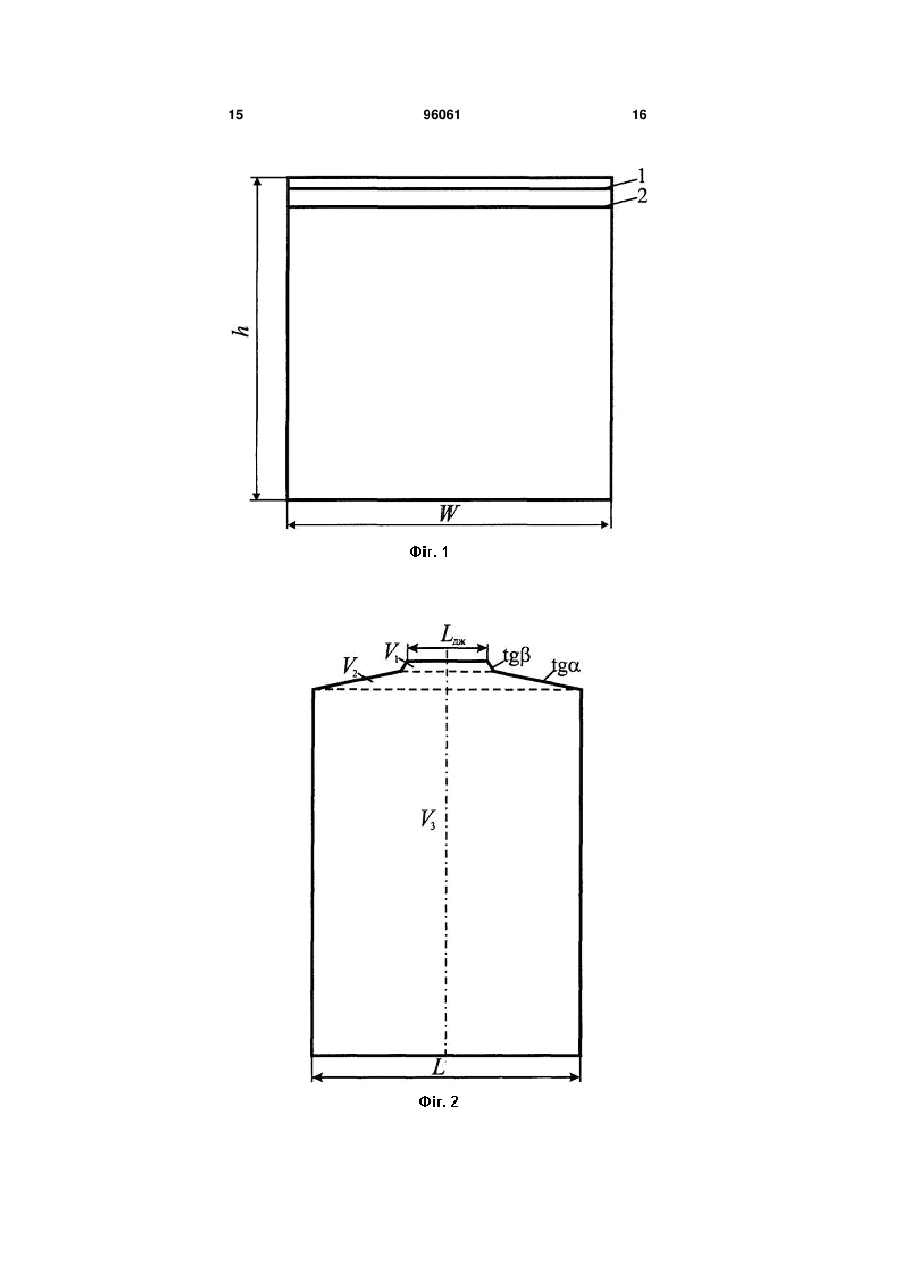
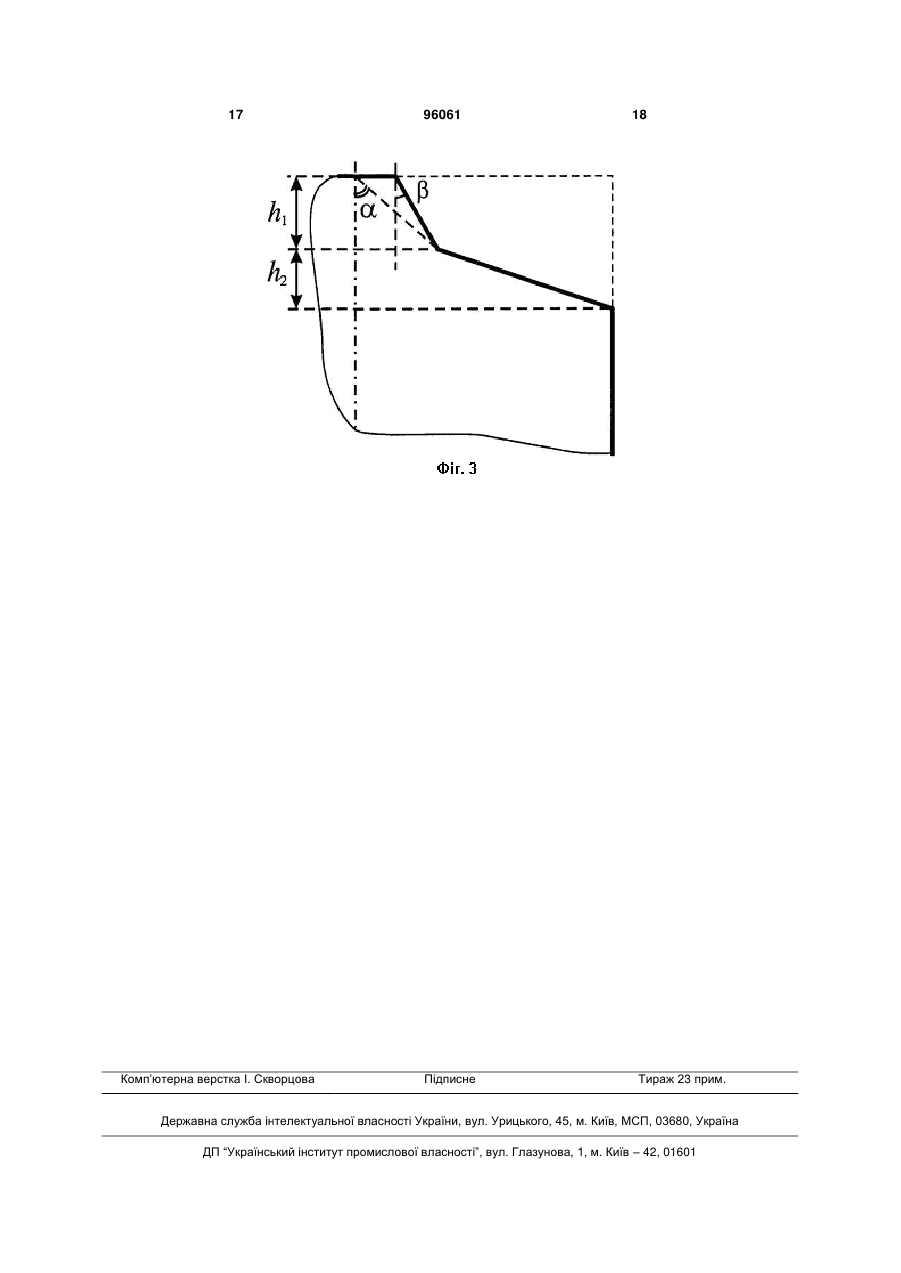
Спосіб визначення теплового опору кристала субмікронного транзистора, що включає вимірювання розмірів фігури теплового еквівалента транзистора від розтікання теплового потоку від затвора всередину кристала під кутами  і  , вимірювання величини елементів теплового екві валента, який відрізняється тим, що вимірюють висоти зломів бокової поверхні фігури теплового еквівалента, а величину теплового опору кристала визначають за формулою: (h  h )(h  h2 ) RT  2 1 , К/Вт, h3   Винахід належить до галузі електронної техніки, а саме до напівпровідникових приладів, і може знайти застосування для експресного визначення температури нагріву субмікронних транзисторів на етапі розробки. Відомі способи визначення контактного термічного опору пластин [1,2]. Суть способів полягає у тому, що запропоновано пристрій, в якому вимірюють температуру на поверхні зразків, що розташовані у тепловому потоці, який тече від джерела тепла до тепловідводу. Термічний опір знаходять за виразом: 1 ,  2 - моменти часу, в які виконуються вимі де RK - термічний опір, К/Вт; Q - коефіцієнт температуропровідності пари 2 зразків, м /с;  - коефіцієнт теплопровідності пари зразків, Вт/(м-К); де Rth - тепловий опір транзистора, К/Вт UCEW - напруга колектор-емітер у нагрітому стані, В; UCEK - напруга колектор-емітер в охолодженому стані, В; C - питома теплоємність матеріалу, К/В; PV - потужність, що розсіюється, Вт. (11) UA 2    t 2 t  16  t1 t 2   t  t   1    1 2   2 2  1  ,  1     2  t1 t 2       2 1    (19) RK    Q  t1 t 2  Q        2   1  рювання температур t1 , t 2 . Відомі способи визначення термічного опору не можуть бути застосовані для визначення теплового опору транзистора через неможливість безпосереднього вимірювання температури на ланках транзистора. Відомий спосіб визначення теплового опору біполярного транзистора з ізольованим затвором [3], який полягає у визначенні теплового опору за формулою: U  UCEK   C R th  CEW , PV 96061 (13) h 2 - висота злому бокової поверхні фігури теплового еквівалента в точках перетину ліній tg з боковими гранями кристала, мкм;  - коефіцієнт теплопровідності матеріалу кристала, Вт/(м  К). C2 де RT - тепловий опір матеріалу кристала, К/Вт; h - висота кристала, мкм; h1 - висота злому бокової поверхні фігури теплового еквівалента в точках перетину ліній tg з лініями tg , мкм; 3 96061 Для визначення теплового опору транзистора за наведеним алгебраїчним виразом необхідно знати електричні параметри напруги колекторемітер для нагрітого UCEW та охолодженого станів UCEK , потужність PV , що розсіюється, питому теплоємність матеріалу C . Однак на етапі розробки і проектування багатошарових легованих структур визначення таких електричних параметрів надто ускладнене. Як прототип прийнято метод визначення теплового опору польового транзистора на GaAs основі з коефіцієнтом теплопровідності  = 30 Вт/(мК), з геометричними розмірами кристала: висотою h = 150 мкм, довжиною L = 400 мкм, шириною W - 400 мкм; з довжиною затвора L ДЖ = 70мкм і ши риною затвора WДЖ =160мкм, описаний в літературному джерелі [3]. Крім того, передбачені кути  і  у вигляді функції tg =1,527 і tg = 0,79 під нахилом яких розтікається тепловий потік від джерела тепла - затвора по кристалу транзистора. Спосіб-прототип по визначенню теплового опору транзистора включає встановлення форми і розмірів фігури теплового еквівалента за слідами розтікання теплового потоку від центра затвору під кутом α і від країв периметра затвора під кутом β; включає вимірювання величини приросту площі перерізів теплового еквівалента по висоті транзистора, величина якого виступає аналогом теплового опору транзистора для кожного елемента висоти, а саме висот зломів бокової поверхні фігури теплового еквівалента, висоти кристала і висот ланцюгів транзистора між кристалом і тепловідводом. Фігуру теплового еквівалента польового транзистора на GaAs основі обмежено зверху площею у формі прямокутника, знизу площею основи кристала в формі квадрата, а бокова поверхня зазнає злому в точках перетину ліній tg з лініями tg , а також в точках перетину ліній tg з боковими поверхнями кристала, по яких тепловий потік стікає до тепловідводу транзистора. Тепловий потік, що розтікається з центру затвора, приймає форму конуса, що обумовлює зломи бокової поверхні теплового еквівалента у формі дуги. Вимірювання площі перерізу теплового еквівалента, що характеризується складною конструкцією, проводять за допомогою аналітичних виразів, які включають подвійні інтеграли за змінними параметрами і гіперболічні функції. Величину приросту площі перерізу теплового еквівалента визначають за формулою: n S   Si1  Si  , i1 де Si - площа перерізу на і-й висоті транзис2 тора, мкм ; n - число перетинів. Величина приросту площі теплового еквівалента в способі-прототипі є аналоговою величиною для визначення теплового опору транзистора для кожного елемента. 4 Недолік способу-прототипу пов'язано зі складностями визначення форми і розмірів теплового еквівалента транзистора і складностями вимірювання площі перерізу фігури теплового еквівалента. У способі, що заявляється, визначення теплового опору кристала транзистора здійснюється за його тепловою моделлю. При цьому графічним способом будують тепловий еквівалент шляхом аналогічним у способі-прототипі і розраховують елементи теплового еквівалента, а саме об'єми і висоти елементів теплового еквівалента і кристала транзистора, які зв'язані з величиною теплового опору. Побудуємо теплову модель для субмікронного транзистора на арсенід-галієвій основі, геометричні розміри якого дорівнюють h  W  L = 100 мкм х 100 мкм х 20 мкм. Джерело тепла (затвор) виконано у вигляді полозка розмірами L ДЖ  WДЖ = 0,6 мкм х 100 мкм. Температурний режим роботи моделі середній: tg = 1,527; tg = 0,819;  = 30 Вт/(м  К) [4]. Теплова модель у вигляді фігури еквівалента наведена на фігурі 1. Будування теплового еквівалента проводять у наступній послідовності. Джерело тепла - полозок, довжиною 0,6 мкм, суміщають з поверхнею кристала і будують кут розтікання теплового потоку  з країв полозка, а кут α - з центральної лінії полозка. Лінії tg і tg формують бокову поверхню теплового еквівалента. Бокова поверхня зазнає злом на висоті h1 при перетині ліній tg з лініями tg і на висоті h 2 при перетині ліній tg з боковими гранями кристала. З вертикальної проекції теплового еквівалента, наведеного на фігуру 2, випливає, що тепловий еквівалент, побудований по слідах розтікання теплового потоку, складається з трьох геометричних фігур, поділених лініями зломів бокової поверхні. Фігура V1 висотою h1 і фігура V2 висотою (h2  h1) являють собою зрізані піраміди, а фігура V3 , - паралелепіпед кристала висотою (h  h2 ) . Зломи бокової поверхні, що розділяють елементи теплового еквівалента, є прямі лінії - лінії 1 і 2 на фіг. 1. На фігурі 3 наведено фрагмент теплового еквівалента з активної зони розтікання теплового потоку. З елементів цієї фігури видно яким чином формується бокова поверхня теплового еквівалента. На першому етапі проводять розрахунок висот зломів поверхні теплового еквівалента h1 і h 2 . Висоту h1 перетину ліній tg з лініями tg визначають за виразом: L ДЖ h1  2  tg L ДЖ 2  tg  tg tg L ДЖ 2 tg 2  tg    tg   ...  0,01    де L ДЖ - довжина джерела тепла, мкм. мкм, 5 96061 6 2 З цього випливає, що висота h1 є сумою спадаючої послідовності елементів з коефіцієнтом tg / tg . S1 - площа трапеції елемента V1 , мкм . V2  S2  W  ((L1  L) / 2)  (h2  h1)  W = = ((1,84+20)мкм/2)-(6,37-0,39)мкм  100мкм= 3 3 =6,35  10 мкм , де S 2 - площа трапеції елемента V2 , мкм. Висоту h 2 перетину тепловим потоком бокових граней кристала визначають за співвідношенням: L h2  2 , мкм, tg де L - довжина кристала, мкм. Далі, відповідно до алгоритма розрахунку, визначають числові значення величин об'ємів елементів, теплового еквівалента. Об'єми елементів V1 і V2 , які являють собою "бруски" довжиною W і які мають у перерізі площину правильної трапеції, визначають за виразами: L ДЖ  L1 3 V1  h W , мкм . 2 L1  L V2   (h2  h1)  W , мкм3, 2 де L1 і L - основи трапецій, мкм. V  V1  V2 =36мкм +6,35  10 мкм = 3 3 =6,39  10 мкм . 2 V3  Sкр(h  h2 ) = 2000мкм  (100  6,37)мкм = 3 2 де Sкр - площа кристала, мкм . Таким чином, повний об'єм теплового еквівалента Vте  V1  V2  V3 . Крім елементів об'ємів теплового еквівалента визначають елементи об'ємів кристала: V 0 - об'єми кристала не зайняті те 3 A V2 A V1  Sкр  h1 , 3 мкм ,  Sкр  (h2  h1) , мкм 3 Знайдемо числові величини елементів теплового еквівалента - фігури теплової моделі субмікронного транзистора. L ДЖ h1   L ДЖ 2  tg 2  tg  tg tg L ДЖ 2 tg =11,96  10 мкм . 3 RT  f V  f R , К/Вт, де f V - безрозмірний коефіцієнт пропорційний тепловому опору; Sкр - коефіцієнт геометричного еквіваf R Vкр   лента теплового опору, що має розмірність К/Вт. Визначимо числове значення теплового опору субмікронного транзистора: f V  f1  f2  f3   h2  2  20мкм / 2  6,37мкм. tg 1,571 V1  S1  W  ((L ДЖ  L1)  h1  W   (( 0,6мкм  184мкм) / 2)  0,39мкм  100мкм  36мкм3 , де L1  L ДЖ  2  h1  tg = 0,6мкм + +2  0,39 мкм  0,819=1,84мкм; A V A  V3 V V2 V3    2  2 Vкр V Vкр Vкр 1196  103 мкм3  187,26  103 , (200  103 )2 (мкм3 )2 Sкр fR  ;  0,056 2000мкм2  . 200  103  30Вт /(м  К )  333,33К / Вт Перетворимо коефіцієнт Sкр LW 1 , К/Вт. fR : fR    Vкр   h  W  L   h   Vкр   V Перетворимо формулу RT  A V2  V3 2 Vкр  f R з ура хуванням того, що A V2  Sкр  (h2  h1) , 2 L ДЖ 3 V 0  V A  V  V A  ( V1  V2 ) = 3 33 3 3 3 =12,74  10 мкм 6,39  10 мкм =6,35  10 мкм . Тепловий опір кристала визначимо за виразом 2 0,6мкм / 2  0,819    мкм  0,39мкм.  1571   ...  0,01  1571 ,  ,  = A V2  Sкр  (h2  h1) = 2000мкм2  (6,37  0,39)мкм =  tg    tg   ...  0,01     0,6мкм / 2 0,6мкм / 2 0,819 / 2    1571 , 1571 , 1571 , 6,37мкм 3 A V1  Sкр  h1 = 2000мкм2  0,39мкм = 780мкм3. висотою V 0 і, V 2A висотою (h2  h1) . 3  =12,74  10 мкм . 3 зона кристала складається з елементів V 0 , V1A мкм , 3 V A  Sкр  h2 =2000мкм2 пловим еквівалентом і V A - об'єми кристала активної зони розтікання теплового потоку. Активна V A  Sкр  h2 , 3 =187,26  10 мкм . 3 Vте  V1  V2  V3 =(36+6,35  10 + 3 3 3 3 +187,26-10 )мкм =193,65  10 мкм . Елемент об'єму V3 , який має у перерізі площу паралелепіпеда висотою (h  h2 ) , визначають за формулою 3 V3  Sкр(h  h2 ) , мкм , 3 V 3  Vкр  V A Rh T Rh  T  Sкр  h  Sкр  h2  Sкр  (h  h2 ) буде (h2  h1)(h  h2 ) h2 Vкр  Sкр  h , мати  тоді вигляд 1 (h  h )(h  h2 )  2 1 , К/Вт. h h3   7 Rh  T  (h2  h1)(h  h2 ) 3 96061 (див. рядок 2.3 табл. 2). Визначено показник кута нахилу зміни величини теплового опору у  h  (6,37  0.39)мкм  (100  6,37)мкм 1003 мкм3  30Вт /(м  К )  18,66К / Вт З формули видно, що для визначення теплового опору кристала субмікронного транзистора треба визначити лише висоти зломів бокової поверхні фігури теплового еквівалента, а числові значення параметрів h і  , є вихідними даними. Порівняльний аналіз операцій способу, що заявляється, і способу-прототипу наведений у таблиці 1. Спільними ознаками двох способів є формування фігури теплового еквівалента за слідами розтікання теплового потоку, вибір величин кутів розтікання теплового потоку  : і  , формування бокової поверхні фігури теплового еквівалента під кутом  від ліній периметра джерела тепла. Відмітними ознаками способу, що заявляється, є формування бокової поверхні фігури теплового еквівалента під кутом α від середньої ліній джерела тепла, визначення висот h1 і h 2 зломів бокової поверхні, розрахунок геометричного еквіR валента теплового опору кристала f , визначення теплового опору кристала. В таблиці 2 наведені приклади визначення теплового опору кристала субмікронного транзистора по способу, що заявляється, при зміні довжини затвору L ДЖ , висоті кристала h , довжині кристала L , теплопровідності напівпровідникового матеріалу кристала  і теплових режимів транзистора. Приклад 1. Величина 18,66 К/Вт складає тепловий опір кристала субмікронного транзистора висотою h = 100 мкм, довжиною L = 20 мкм, шириною W =100 мкм, довжиною затвору L ДЖ = 0,6 мкм для середнього теплового режиму нагріву ( tg = 1,571; tg = 0,819;  = 30 Вт/(м  К)), розрахунок якого докладно розглянуто в описі способу, що заявляється. Розраховані висоти h1 = 0,39 мкм і h2 = 6,37 мкм (рядки 1.1 і 1.2 табл. 2), об'єми V3 3 3 3 3 A = 187,26  10 мкм і V2 = 11,96  10 мкм (рядки 1.6 і 1.8 табл. 2), коефіцієнти пропорційності f R = 333,33 К/Вт f V  f h = 0,05597 (рядки 1.10-1.12 табл.2), з яких розраховують величину теплового опору кристала субмікронного транзистора по співвідношенню (h  h )(h  h2 ) RT  2 1 (рядок 1.15 табл. 2) h3   Приклад 2. Наведені теплові опори субмікронного транзистора для двох значень довжини затвора L ДЖ = 0,3 мкм і L ДЖ =1,2 мкм. Опис прикладу подібний опису прикладу 1 табл. 2, в якому L ДЖ = 0,6 мкм. Розраховані числові величини RT |L ДЖ 0,3мкм =19,25 К/Вт і RT |L ДЖ 1,2мкм =17,54 К/Вт 8 вигляді функцій  L ДЖ  R T / L ДЖ =-1,53 К/Вт на 1 мкм зміни довжини джерела тепла (див. рядок 2.4 табл. 2), який вказує на обернено пропорційну залежність теплового опору від довжини затвора. Приклад 3. Визначено числові величини теплового опору кристала транзистора для висот h = 80 мкм і h = 120 мкм. Опис прикладу подібний опису прикладу 1 табл.2, в якому h = 100 мкм. Розраховані величини RT |h80мкм = 28,66К/Вт і RT |h120 мкм =13,11К/Вт (див. рядок 3.4 табл. 2). L Показник  ДЖ  RT / h =-0,38 К/Вт на 1 мкм зміни висоти (див. рядок 3.5 табл. 2), при цьому спостерігається обернено пропорційна залежність теплового опору від висоти кристала. Приклад 4. Наведені числові значення величини теплового опору кристала транзистора для довжин L = 15 мкм і L = 30 мкм. Опис прикладу подібний опису прикладу 1 табл. 2, в якому L = 20 мкм. Розраховані величини RT |L 15мкм = 13,93 К/Вт RT |L30мкм = 27,61К/Вт (див. рядок 4.5 табл. 2). Для цього діапазону L змін елемента визначено показник L  RT / L 1=0,91 К/Вт на 1 мкм зміни довжини кристала (див. рядок 4.6 табл. 2), при цьому спостерігається прямо пропорційна залежність теплового опору від довжини кристала. Приклад 5. Наведені числові значення величини теплового опору кристала транзистора для різних значень теплопровідності матеріалу кристала  = 25 Вт/(м  К) і  = 35 Вт/(м  К). Опис прикладу подібний опису прикладу 1 табл. 2, в якому теплопровідності матеріалу кристала  = 30 Вт/(м  К). Розраховані величини і RT | 25Вт /(мК ) = 22,4 К/Вт і RT | 35Вт /( мК ) = 15,99 К/Вт (див. рядок 5.3 табл. 2). Для цього діапазону змін елемента  визначено показник    RT /  = -0,64 К/Вт на одиницю зміни теплопровідності матеріалу кристала (див. рядок 5.4 табл. 2), при цьому спостерігається обернено пропорційна залежність теплового опору від теплопровідності матеріалу кристала. Приклад 6. Розрахована величина теплового опору кристала транзистора для ізотермічного і максимального теплових режимів, за рахунок вибору тангенсів кутів розтікання теплового потоку. Для ізотермічного теплового режиму: tg = 1,055; tg = 1,571, для максимального теплового режиму tg = 0,373; tg = 1,571. Опис прикладу подібний опису прикладу 1 табл. 2 для середнього теплового режиму, в якому tg = 0,819; tg = 1,571. Встановлено величину RТіз = 18,63 К/Вт і величину RТ max = 19,1 К/Вт (див. рядок 6.6 табл. 2), RТсер = 18,66 К/Вт (див. рядок 1.15 табл. 2). 9 З наведених в таблиці 2 прикладів розрахунку теплового опору кристала субмікронного транзистора видно, що тепловий опір прямо пропорційно залежить від зміни довжини кристала і обернено пропорційно - від зміни довжини затвора, висоти кристала і коефіцієнта теплопровідності матеріалу кристала; RТ max менше RТсер , а RТ max більше RТсер . Результати способу визначення теплового опору кристала субмікронного транзистора при зміні вихідних параметрів транзистора, наведені в прикладах 1-6, показують можливість застосування його для визначення теплового опору кристала по формулі: (h  h )(h  h2 ) RT  2 1 , К/Вт, h3   де RT - тепловий опір матеріалу кристала, К/Вт; h - висота кристала, мкм; 96061 10 h1 - висота злому бокової поверхні фігури теплового еквівалента в точках перетину ліній tg з лініями tg , мкм; h 2 - висота злому бокової поверхні фігури теплового еквівалента в точках перетину ліній tg з боковими гранями кристала, мкм;  , - коефіцієнт теплопровідності матеріалу кристала, Вт/(м  К). Спосіб, що заявляється, має наступні переваги: тепловий еквівалент субмікронного транзистора з затвором у формі полозка наведено у вигляді сукупності простих геометричних фігур, що дозволяє легко розраховувати параметри цих фігур (висоти, площі, об'єми); для визначення теплового опору кристала субмікронного транзистора достатньо визначити лише висоти зломів бокової поверхні теплового еквівалента. Таблиця 1 Порівняльний аналіз операцій способу-прототипу і способу, що заявляється № п/п 1 2 3 4 5 6 7 8 9 10 11 12 13 Назва операцій Формування фігури теплового еквівалента за слідами розтікання теплового потоку Обґрунтування вибору величин кутів розтікання теплового потоку  і  Формування бокової поверхні фігури теплового еквівалента під кутом  від ліній периметра джерела тепла Формування бокової поверхні фігури теплового еквівалента під кутом  від центру джерела тепла Формування бокової поверхні фігури теплового еквівалента під кутом  від середньої лінії джерела тепла Визначення висоти злому h1 при перетині ліній tg 3 з лініями tg Визначення висоти злому h 2 при перетині ліній tg з боковими гранями кристала Визначення площі перерізу фігури теплового еквівалента на і-му кроці Приріст площі перерізу S  Si1  Si S Визначення теплового опору fT  k  S , К/Вт, де k - коефіцієнт пропорційності Розрахунок геометричного еквівалента теплового опору кристала , К/Вт fR  1 (h  ) Розрахунок безрозмірного еквівалента теплового опору кристала f V  f1  f2  f3 Визначення теплового опору кристала RT  f R  f V , K/BT Спосібпрототип Спосіб, що заявляється так так так так так так так ні ні так ні так ні так так так ні ні так ні ні так ні так ні так 11 96061 12 Таблиця 2 Параметри субмікронного транзистора базової моделі № п/п 0 01 02 Формули визначення елементів теплового еквівалента Результат Вихідні дані субмікронного транзистора з кристалом із GaAs 3 Висота, довжина, ширина кристала h х Lx W мкм 2 Довжина і ширина затвора L ДЖ х WДЖ мкм 100 × 20 × 100 0,6 × 100 Теплопровідність матеріалу кристала  Вт/(м  К) Тепловий режим середній: 04 Величина tg 05 Величина tg 1 Розрахункові параметри базової моделі 1.1 h1  L ДЖ / 2 / tg  L ДЖ / 2 / tg  tg / tg  ...  0,01 мкм 03 30 1,571 0,819 0,39 1.2 h2  l / 2 / tg  20 / 2 / 1571 мкм , 1.3 L1  L ДЖ  2  h1  tg  0,6  2  0,39  0,819 мкм 1.4 V1  (L ДЖ  L1) / 2  h1  W  (0,6  124) / 2  0,30  100 х10 мкм , 1.5 V2 (L1  L) / 2  (h2  h1)  W  (124  20) / 2  5,98  100 х10 мкм , 1.6 V3  Sкр  (h  h2 )  W  L  (h  h2 )  20  100  93,63 х10 мкм 1.7 V  V1  V2  (0,36  6,35) х10 1.8 1.9 6,37 1,24 3 3 3 3 3× 3 10 мкм 187,26 6,386 V V2  Sкр  (h2  h1)  W  L  (h2  h1)  200  (6,37  0,39) 10 мкм V 6,35 3 3 3 A 0,036 3  Sкp  h2  W  L  h2  200  6,37 х10 мкм 3 3 11,96 3 12,74 1.10 f R  1/(h  )  1/ 100  106  30 К/Вт V 1.11 f  A V V2 V3 VA  V 1196  103  187,26  103 ,    2 2 3  Vкр V Vкр Vкр (200  103 )2 (мкм3 )2 f h  fV  1.12  333,33 A V2  V3 2 Vкр  (h2  h1)( h  h2 ) h2 Sкр(h2  h1)  Sкр(h  h2 )  (Sкр  h)2 0,05597  0,05597 ( 6,37  0,39)(100  6,37) 1002 V 1.13 RT  f R  f V = 333,33-0,05597 К/Вт 18,66 1 (h2  h1)(h  h2 ) (h2  h1)(h  h2 )   h h2 h3   кВт (6,37  0,39)(100  6,37) Rh  f R  f h  T 1.14  1.15 RT  2 18,66 1003  30 (h2  h1)(h  h2 ) h3   Числові значення величин елементів теплового еквівалента базової моделі при різних довжинах затвора L ДЖ 0,3 1,2 2.1 h1  L ДЖ / 2 / tg  L ДЖ / 2 / tg  tg / tg  ...  0,01мкм 0,2 0,75 2.2 h2  L / 2 / tg  20 / 2 / 1527 мкм , 6,37 6,37 19,25 17,54 3 2.3 RT  (h2  h1)(h  h2 ) /(h   ) К/Вт 2.4  L ДЖ  RT / L ДЖ  (19,25  17,54) /(0,3  1 2)  153 К/Вт на 1 довжини джерела тепла мкм , , Числові значення величин елементів теплового еквівалента базової моделі при різних висотах кристала h мкм 3.1 h1  L ДЖ / 2 / tg  L ДЖ / 2 / tg  tg / tg  ...  0,01 мкм 3 80 120 0,39 0,39 3.2 h2  L / 2 / tg  20 / 2 / 1527 мкм , 6,37 6,37 3.3 h  h2 мкм 73,63 113,63 13 96061 14 Продовження таблиці 2 3.4 RT  (h2  h1)(h  h2 ) /(h3   ) кВт 3.5 h  RT / h  (28,66  13,11) /(80  120)  0,38 К/Вт на 1 мкм висоти кристала 28,66 Числові значення величин елементів теплового еквівалента базової моделі при різних довжинах кристала L мкм 4.1 h1  L ДЖ / 2 / tg  L ДЖ / 2 / tg  tg / tg  ...  0,01 мкм 4 13,11 15 30 0,39 0,39 4.2 h2  L / 2 / tg мкм 4,77 9,55 4.3 h2 h1 мкм 4,38 9,16 4.4 h  h2 мкм 95,23 90,45 13,9 27,62 25 35 0,39 0,39 6,37 6,37 22,4 15,99 3 4.5 RT  (h2  h1)(h  h2 ) /(h   ) К/Вт 4.6 L  RT / L  (27,62  13,9) /(30  15)  0,91 К/Вт на 1 мкм довжини кристала Числові значення величин елементів теплового еквівалента базової моделі при різних значеннях теплопровідності матеріалу кристала  Вт/(м-К) 5.1 h1  L ДЖ / 2 / tg  L ДЖ / 2 / tg  tg / tg  ...  0,01мкм 5 5.2 5.3 5.4 h2  L / 2 / tg  20 / 2 / 1527 мкм , 3 RT  (h2  h1)(h  h2 ) /(h   ) К/Вт    RT /   (22,4  15,99) /(25  35)  0,64 К/Вт на одиницю теплопровідності матеріалу кристала Числові значення елементів теплового еквівалента базової моделі для ізотермі- R Tіі чного і максимального теплових режимів 6.1 Величина tg 1,055 6.2 Величина tg 1,571 6.3 Коефіцієнт відношення tg / tg 0,67 h1  L ДЖ / 2 / tg  L ДЖ / 2 / tg  tg / tg  ...  0,01 мкм 6.4 0,38 6 6.5 6.6 h2  L / 2 / tg  20 / 2 / 1527 мкм , 3 RT  (h2  h1)(h  h2 ) /(h   ) К/Вт Позначення: RT - тепловий опір кристала транзистора, К/Вт; RТсер , RT max , RТіз тепловий опір кристала для середнього, максимального й ізотермічного теплових режимів, відповідно, К/Вт; A V1, V 2, V3, V, V A , V2 - елементи фігури теп3 лового еквівалента, мкм ; h1, h2 - висоти зломів бокової поверхні кристала транзистора, мкм; h - висота кристала, мкм; Sкр - площа крис тала, мкм;  - коефіцієнт теплопровідності матеріалу кристала, Вт/(м  К); f R - геометричний коефіцієнт пропорційності, К/Вт; f V , f h - безрозмірний коефіцієнт пропорційності;  - показник зміни теплового опору кристала; RT max 0,373 1,571 0,24 0,25 6,37 6,37 18,69 19,10 tg - тангенс кута розтікання теплового потоку з середньої лінії затвора; tg - тангенс кута розтікання теплового потоку з країв затвора. Джерела інформації: 1. Авторское свидетельство СССР, № 5 1800344 (Al), кл. МПК G01N25/18 Способ определения контактного термического сопротивления 07.03.93. Бюл. № 9. 2. Авторское свидетельство СССР, № 5 1582101 (А1), кл. МПК G01N25/18 Способ определения контактного термического сопротивления 07.03.93. Бюл. № 9. 3.Pat.FR DE38322730Al29.03.90Verfahren und Anordnung zur bestimmung des warmewiderstandes 5 von IGBT-Bauelementen IPC G01N25/18 4. Захоров А. Л., Асвадурова Е. И. Расчет тепловых параметров полупроводниковых приборов: Метод эквивалентов. - М.: Радио и связь, 1983.-184 с. (6.3. С. 125-134). 15 96061 16 17 Комп’ютерна верстка І. Скворцова 96061 Підписне 18 Тираж 23 прим. Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601