Відмовостійка система кутової стабілізації мультироторного літального апарата

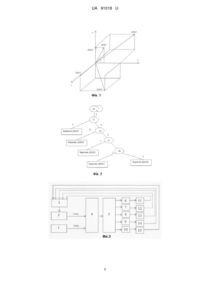
Реферат: Відмовостійка система кутової стабілізації мультироторного літального апарата містить три датчики кутових швидкостей та аналого-цифровий перетворювач, чутливі осі перших двох датчиків співпадають з двома осями ортогональної системи координат. Додатково містить два датчики кутових швидкостей, при цьому вісь третього датчика кутової швидкості направлена під кутом відносно до третьої ортогональної осі, осі четвертого та п'ятого датчиків кутових швидкостей направлені з початку координат по діагоналі куба в 2 та 4 октанти відповідно, виходи датчиків кутових швидкостей послідовно через відповідно інтегратори, аналогоцифровий перетворювач, а також блок діагностування, паралельно із задавальним пристроєм, підключені до блока формування кутових швидкостей двигунів мультироторного літального апарата. UA 91018 U (12) UA 91018 U UA 91018 U 5 10 15 20 25 30 35 40 45 50 Корисна модель належить до області космонавтики і може бути використана при проектуванні систем стабілізації мультироторного літального апарата. Відомий відмовостійкий блок датчиків кутових швидкостей мультироторного літального апарата [див. патент №UA65275 G05D1/08. Відмовостійкий блок вимірювачів параметрів руху мультироторного літального апарата, Джулгаков В.Г., Руденко К.І., Вєдєрнікова О.Г., Винник К.В., Кісс Д.С.], узятий як прототип, що містить три датчики, розташовані по осях координат, три акселерометри для вимірювання лінійних прискорень, головний вимірювальний мікроконтролер та аналого-цифровий перетворювач, входи якого зв'язані з датчиками кутової швидкості і акселерометрами, а вихід підключено до головного вимірювального мікроконтролера, та два розташовані у перпендикулярних площинах інтегровані компаси-висотоміри, виходи яких зв'язані з головним вимірювальним мікроконтролером та дублюючим вимірювальним мікроконтролером, які з'єднані з центральним обчислювальним модулем по окремих локальних інформаційних шинах, а в корпус кожного датчика кутової швидкості вбудовані датчики температури, виходи яких підключені до аналого-цифрового перетворювача, вбудованого в головний вимірювальний мікроконтролер, який з'єднаний з модулем для зв'язку з комп'ютером по інтерфейсу USB. До недоліків такої системи належать надмірна надлишковість, відсутність резервних датчиків кутових швидкостей, що не дозволяє забезпечити резервування, необхідність формування дискретних сигналів активації режиму самотестування ДКШ. Задачею корисної моделі є підвищення надійності мультироторного літального апарата (МЛА) відносно існуючих систем стабілізації, а також підвищення точності. Поставлена задача вирішується тим, що в відмовостійкій системі кутової стабілізації мультироторного літального апарата, що містить три датчики кутових швидкостей та аналогоцифровий перетворювач, чутливі осі перших двох датчиків співпадають з двома осями ортогональної системи координат, згідно із корисною моделлю, додатково введено два датчики кутових швидкостей, при цьому вісь третього датчика кутової швидкості направлена під кутом відносно до третьої ортогональної осі, осі четвертого та п'ятого датчиків кутових швидкостей направлені з початку координат по діагоналі куба в 2 та 4 октанти відповідно, виходи датчиків кутових швидкостей послідовно через інтегратори, аналого-цифровий перетворювач, а також блок діагностування, паралельно із задавальним пристроєм, підключені до блока формування кутових швидкостей двигунів мультироторного літального апарата. На Фіг. 1 показане розташування осей БІНС МЛА із мінімальною структурною надмірністю, на Фіг. 2 представлений фрагмент дихотомічного дерева визначення місця відмови в відмовостійкій системі кутової стабілізації мультироторного літального апарата, на Фіг. 3 представлена функціональна схема відмовостійкої системи кутової стабілізації мультироторного літального апарата. Запропонована відмовостійка система кутової стабілізації мультироторного літального апарата складається із п'яти датчиків кутової швидкості 6-10, які послідовно підключені відповідно через інтегратори 11-15 та аналого-цифровий перетворювач 2, вхід якого підключені до входу блока діагностування 3, паралельно із задавальним пристроєм 1 до блока формування кутових швидкостей 4 мультироторного літального апарата 5. Відмовостійка система кутової стабілізації мультироторного літального апарата працює таким чином. На виході датчиків кутових швидкостей МЛА формуються сигнали у вигляді напруги постійного струму, датчики через інтегратори підключені до аналого-цифрового перетворювача, що підключений до блока діагностування, який, відповідно до діагностичного 45 дерева, приймає рішення щодо справності датчиків та передає інформацію про кутове положення літального апарата до блока формування кутових швидкостей літального апарата, який, в свою чергу, формує керуючий вплив на літальний апарат на підставі інформації про необхідне та фактичне положення літального апарата у просторі. На підставі цього введемо наступні позначення: U1, U2, U3, U4, U5 - значення напруг на виходах датчиків 6, 7, 8, 9, 10 50 відповідно в к-й момент часу. З огляду на розташування датчиків (Фіг. 1) маємо наступні рівняння для датчиків кутової швидкості: 1 UA 91018 U   U ( t )  1  ( t )  3  ( t )  0 ( t ) x y z  1 2 2  U2 ( t )  0x ( t )  1 y ( t )  0z ( t )  U3 ( t )  0x ( t )  0 y ( t )  1z ( t )  U ( t )  1  ( t )  1  ( t )  1  ( t ) x y z  4 3 3 3  U ( t )  1  ( t )  1  ( t )  1  ( t ) x y z  5 3 3 3  , (1) де - проекції кутової швидкості обертання на осі зв'язаної системи координат. Систему рівнянь 1 перепишемо в вигляді матричного добутку:   U1( t )      U2 ( t )  U3 ( t )      U4 ( t )  U ( t )   5     5 1 2 0 3 2 1 0 1 0 1  3 1 1 3 3 3  0   0   ( t ) x 0   ( t )  y  1   3  z ( t ) 1    3  . (2) Позначимо:      K       1 2 0 3 2 1 0 1 0 1  3 1 1 3 3 3  0   0  0  1   3  1    3  . (3)  Дослідимо дану матрицю по критерію повного діагностування. З (3) видно, що всі рядки матриці. К лінійно незалежні, тобто потрібно перевірити другу умову для всіх симетричних матриць А(3 × 3) з матриці К. C3  5 10 15 20 25 30 5!  10 3 ! 2! матриць A i , i  1...10. Маємо Розглянемо ці матриці: A1=(U1,U2,U3); A2=(U1,U2,U4); A3=(U1,U2,U5); A4=(U2,U3,U4); A5=(U2,U3,U5); A6=(U3,U4,U5); A7=(U1,U3,U4); A8=(U1,U3,U5); A9=(U1,U4,U5); A10=(U2,U4,U5). (4) Розрахуємо детермінант кожної матриці: detA1=0,5; detA2=0,2887; detA3=-0,2887; detA4=0,5774; detA5=0,2887; detA6=0,667; detA7=0,7887; detA8=0,2113; detA9=0,5774; detA10=0,6667. (5) 2 UA 91018 U 5 10 3 (5) видно, що всі детермінанти матриці не дорівнюють нулю, тобто даний блок, який складається з п'яти датчиків, може бути повністю діагностований. Для розрахунку запропонованої корисної моделі складемо логічну таблицю для формування предикатів діагностування. Можна скласти 5 множин рівнянь, причому з кожної множини можна формулювати показники з одного датчика через всі інші з другої множини. Позначимо такі множини як: S1=(U1,U2,U3, U4); S2=(U1,U2,U3, U5); S3=(U2,U3,U4, U5); S4=(U1,U3,U4, U5); S5=(U1,U2,U4, U5). (6) Розглянемо множину S1=(U1,U2,U3, U4). Складемо систему рівнянь:  1 3  y ( t )  0 z ( t ) U1( t )  x ( t )  2 2  U2 ( t )  0x ( t )  1y ( t )  0z ( t )   U3 ( t )  0x ( t )  0y ( t )  1z ( t )  1 1 1 U4 ( t )  x ( t )  y ( t )  z ( t )  3 3 3  . (7) 15 З системи рівнянь (7) маємо:  ( t )  2U ( t )  3 U ( t ) 1 2  x y ( t )  U2 ( t )  z ( t )  U3 ( t )  U ( t )  1  ( t )  1  ( t )  1  ( t ) x y z  4 3 3 3  . (8) 3 (8) випливає: 1 U4 ( t )  3 Або 20 U1( t )  1 2 2U (t)  1  1 3 U2 ( t )   3 U (t)  ( U2 ( t )  3 1 3 U3 ( t ) . (9)  (10) 3  1)U2 ( t )  U3 ( t ) 4 3 (10) можна позначити як оцінне значення по датчику ДКШ1, тобто:  1 ~ U1( t )  U1( t )  2 ~  3 U (t)  (  . (11) ~ ~ 3  1)U2 ( t )  U3 ( t ) 4 Тобто, якщо всі датчики справні, то  1 ~ ~ U1( t )  U1( t )  U1( t )  2 25 ~  3 U (t)  ( 4  ~ ~ 3  1)U2 ( t )  U3 ( t )  0 . (12) Аналогічно ведуться розрахунки для чотирьох інших множин S2, S3, S4 та S5. Після проведених розрахунків отримаємо:  1 ~ ~ 1  U1( t )  U1( t )  U1( t )  2  ~ ~  2  U2 ( t )  U2 ( t )  U2 ( t )  ~  3 U (t)  ( 4 1 1 3   ~ ~ 3  1)U2 ( t )  U3 ( t )  0  ~ ~ ~ 3 U5 ( t )  2U1( t )  U3 ( t )  0 , (13) , (14)   3~  3~ ~ ~ ~  3  U3 ( t )  U3 ( t )  U3 ( t )   U4 ( t )  U5 ( t )  U2 ( t )  0 2  2    , (15)  ~ ~  4  U4 ( t )  U4 ( t )  U4 ( t )  30  1 ~ ~ 4U (t)  2 3 U (t)  (3  3 1 1 3    ~ 3 )U5 ( t )  0 , (16) 1 ~ ~ ~ ~ ~ 5  U5 ( t )  U5 ( t )  U5 ( t )  4 U1( t )  2 3 U3 ( t )  3U5 ( t )  0 3 . (17) Розглянемо вплив відмови кожного датчика на тотожностях (13-17): 3 UA 91018 U 5 10 Якщо відбулася відмова ДКШ1, то тотожності (13), (14), (16), (17) дорівнюють нулю. Якщо відбулася відмова ДКШ2, то тотожності (13), (14), (15), (17) дорівнюють нулю. Якщо відбулася відмова ДКШ, то тотожності (13), (14), (15), (16) дорівнюють нулю. Якщо відбулася відмова ДКШ4, то тотожності (13), (15), (16), (17) дорівнюють нулю. Якщо відбулася відмова ДКШ5, то тотожності (14), (15), (16), (17) дорівнюють нулю. З проведеного вище аналізу формуємо наступні предикатні рівняння: руйнуються, тобто руйнуються, тобто руйнуються, тобто руйнуються, тобто руйнуються, тобто 1  немавідмови Z0  S 0  0   0  відмова 1  відмова ДКШ5  Z1  S1  0    0  відмова ДКШ1 або ДКШ2, або ДКШ3, або ДКШ4     1  відмова ДКШ4 Z 2  S  2  0   0  відмова ДКШ1 або ДКШ2 або ДКШ3   1  відмова ДКШ1  Z 3  S  3  0   0  відмова ДКШ2 або ДКШ3   15   1  відмова ДКШ1  Z 4  S  4  0   0  відмова ДКШ3  .  20 25 30 35 40  Отримані предикатні рівняння дають змогу сформулювати алгоритм для розв'язання першого та другого завдання діагностування виявлення відмов за допомогою предикату та виявлення місця відмови за допомогою предикатів. Це дозволяє представити рішення важливого завдання при побудові діагностичного забезпечення побудові правил пошуку місця відмов (ППМ) у відмовостійкій системі кутової стабілізації мультироторного літального апарата. Рішення цього завдання засновано на одержанні безумовних ППМ. Розроблене діагностичне дерево (див Фіг. 2) у рамках сигнальнопараметричного підходу дозволяє вирішувати два найбільш важливих завдання діагностування технічного стану МЛА установлення факту виявлення відмовив системі і визначення місця його виникнення. Таким чином, поставлені завдання повністю вирішуються. Корисна модель дозволяє підвищити точність і надійність відмовостійкості системи кутової стабілізації мультироторного літального апарата. ФОРМУЛА КОРИСНОЇ МОДЕЛІ Відмовостійка система кутової стабілізації мультироторного літального апарата, що містить три датчики кутових швидкостей та аналого-цифровий перетворювач, чутливі осі перших двох датчиків співпадають з двома осями ортогональної системи координат, яка відрізняється тим, що містить додатково два датчики кутових швидкостей, при цьому вісь третього датчика кутової швидкості направлена під кутом відносно до третьої ортогональної осі, осі четвертого та п'ятого датчиків кутових швидкостей направлені з початку координат по діагоналі куба в 2 та 4 октанти відповідно, виходи датчиків кутових швидкостей послідовно через відповідно інтегратори, аналого-цифровий перетворювач, а також блок діагностування, паралельно із задавальним пристроєм, підключені до блока формування кутових швидкостей двигунів мультироторного літального апарата. 4 UA 91018 U 5 UA 91018 U Комп’ютерна верстка О. Рябко Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 6