Спосіб визначення діючих значень періодичного несинусоїдального струму і його непарних гармонік шляхом множення залежностей струму від часу на гратчасту дельта-функцію з різними інтервалами дискретизації
Номер патенту: 102741
Опубліковано: 12.08.2013
Автори: Середа Олександр Григорійович, Кобозєв Олександр Сергійович
Формула / Реферат
Спосіб визначення діючих значень періодичного несинусоїдального струму i його непарних гармонік шляхом множення залежностей струму в часі на ґратчасту дельта-функцію з різними інтервалами дискретизації за допомогою модулів мікропроцесора апарата захисту електричних кіл, у якому параметри електричного кола, необхідні для побудови апаратів та систем релейно-струмового захисту мереж електропостачання, а саме діюче значення несинусоїдального фазного струму ![]() , визначають методом чисельного інтегрування, в діапазоні часу від 0 до значення, що дорівнює періоду зміни струму першої гармоніки
, визначають методом чисельного інтегрування, в діапазоні часу від 0 до значення, що дорівнює періоду зміни струму першої гармоніки ![]() , квадратів тих миттєвих значень фазного струму
, квадратів тих миттєвих значень фазного струму ![]() , отриманих з датчиків струму, що відповідають дискретним значенням результату множення залежності зміни фазного струму в часі
, отриманих з датчиків струму, що відповідають дискретним значенням результату множення залежності зміни фазного струму в часі ![]() на ґратчасту δ-функцію
на ґратчасту δ-функцію ![]() , де інтервал дискретизації
, де інтервал дискретизації ![]() ґратчастої функції в три і більше разів менший за період
ґратчастої функції в три і більше разів менший за період ![]() зміни струму найвищої k-ї непарної гармоніки струму
зміни струму найвищої k-ї непарної гармоніки струму ![]() , який відрізняється тим, що в апараті захисту додатково застосовують поєднаний з датчиками струмів мікропроцесорний розчіплювач, в якому здійснюють множення залежності зміни фазного струму в часі
, який відрізняється тим, що в апараті захисту додатково застосовують поєднаний з датчиками струмів мікропроцесорний розчіплювач, в якому здійснюють множення залежності зміни фазного струму в часі ![]() на ґратчасту δ-функцію
на ґратчасту δ-функцію ![]() , при цьому інтервал дискретизації ґратчастої δ-функції
, при цьому інтервал дискретизації ґратчастої δ-функції ![]() в два рази менший за період зміни струму n-ї гармоніки, де
в два рази менший за період зміни струму n-ї гармоніки, де ![]() k,
k, ![]() ,
, ![]() , 1 - номер непарної гармоніки, після чого методом чисельного інтегрування квадратів тих миттєвих значень струму, які відповідають дискретним значенням результату множення залежності зміни фазного струму в часі
, 1 - номер непарної гармоніки, після чого методом чисельного інтегрування квадратів тих миттєвих значень струму, які відповідають дискретним значенням результату множення залежності зміни фазного струму в часі ![]() на ґратчасту δ-функцію
на ґратчасту δ-функцію ![]() , визначають діюче значення струму без урахування найбільшої k-ї гармоніки, тобто струму
, визначають діюче значення струму без урахування найбільшої k-ї гармоніки, тобто струму ![]() , в якому найвищою є
, в якому найвищою є ![]() гармоніка, після чого визначають діюче значення струму k-ї гармоніки
гармоніка, після чого визначають діюче значення струму k-ї гармоніки ![]() з виразу
з виразу ![]() , потім, для визначення діючого значення наступної більш низької,
, потім, для визначення діючого значення наступної більш низької, ![]() -ї гармоніки струму
-ї гармоніки струму ![]() , здійснюють множення залежності від часу струму k-ї гармоніки, що виражається залежністю
, здійснюють множення залежності від часу струму k-ї гармоніки, що виражається залежністю ![]() , на ґратчасту δ-функцію
, на ґратчасту δ-функцію ![]() , після чого отримані дискретні значення струму k-ї гармоніки
, після чого отримані дискретні значення струму k-ї гармоніки ![]() віднімають з миттєвих значень струму
віднімають з миттєвих значень струму ![]() , які відповідають дискретним значенням результату множення залежності зміни фазного струму у часі
, які відповідають дискретним значенням результату множення залежності зміни фазного струму у часі ![]() на ґратчасту δ-функцію
на ґратчасту δ-функцію ![]() , потім отримані миттєві значення струму
, потім отримані миттєві значення струму ![]() зводять в квадрат і методом їх чисельного інтегрування отримують діюче значення струму
зводять в квадрат і методом їх чисельного інтегрування отримують діюче значення струму ![]() , в якому найвищою є
, в якому найвищою є ![]() гармоніка, після чого визначають діюче значення струму
гармоніка, після чого визначають діюче значення струму ![]() -ї гармоніки
-ї гармоніки ![]() з виразу
з виразу ![]() , після цього аналогічним методом визначають діюче значення наступних, нижчих гармонік з виразу
, після цього аналогічним методом визначають діюче значення наступних, нижчих гармонік з виразу 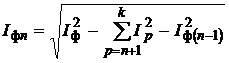 .
.
Текст
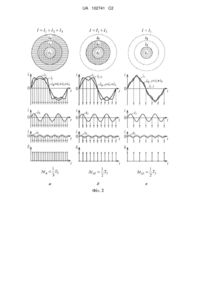
Реферат: Винахід належить до способів визначення параметрів електричних кіл, зокрема гармонійної характеристики чотиридротяної мережі 0,4 кВ з нелінійними видами навантажень. Задача винаходу - розробка способу визначення діючих значень періодичного несинусоїдального фазного струму Iф , який за рахунок вибору часового інтервалу дискретизації ґратчастої дельта-функції, що відповідає додатковому значенню, дозволяє визначати як діюче значення суми усіх гармонік фазного струму Iф , так і діючі значення струмів Iфn кожної з n гармонік, а також знизити необхідну для цього кількість математичних операцій порівняно з існуючими методами. Для цього, до відомого способу, в якому інтервал дискретизації залежності фазного струму від часу i ф f t визначають в 3 і більше разів менший за період Tk зміни струму найвищої k ї непарної гармоніки струму, визначають інтервали дискретизації в 2 рази меншими за період зміни струму кожної n ї гармоніки. В останньому випадку діюче значення струму визначається без урахування струму n ї гармоніки, що дозволяє за рахунок достатньо простих математичних операцій визначити діюче значення струму n-ї гармоніки. UA 102741 C2 (12) UA 102741 C2 UA 102741 C2 5 10 15 Винахід належить до способів визначення параметрів електричних кіл, зокрема, гармонійної характеристики чотирьох провідної мережі електропостачання напругою 0,4 кВ з нелінійними видами навантажень. Необхідність визначення як кількості гармонійних складових струму, так і їх діючих значень, обумовлена тим, що при використанні мікропроцесорної техніки для побудови нових систем релейно-струмових захистів все ширше використовують комплексні критерії спрацьовування цих захистів, які поєднують не один, а декілька параметрів електричного кола, що захищається. Так, наприклад, при реалізації технічного рішення [1] захисту від струмів віддалених коротких замикань, критерій спрацьовування такого захисту є комплексним, в який, окрім величини струму I електричного кола, що захищається, додані також значення коефіцієнта потужності цього кола cos та вид струму збурення (дво або трифазний). При реалізації захисту від можливих перенапруг у однофазних споживачів у разі обриву нейтрального провідника (Nпровідника) і надмірної несиметрії фазних струмів Iф [2], як критерій спрацьовування такого захисту використовують наступні параметри електричного кола: фактична величина струму в Nпровіднику IN, яка визначається з миттєвих значеннях фазних струмів; очікувана величина струму в N-провіднику I / , що визначається за значеннями несиметрії фазних струмів; значення N струмів в аварійній частині електричного кола та інші. У запропонованому в [2] технічному рішенні захисту від можливих перенапруг у разі обриву N-провідника факт його обриву визначався шляхом порівняння фактичного значення струму в 20 N-провіднику IN і очікуваного значення I / , яке визначається як геометрична сума фазних N струмів Iф. Такий підхід справедливий по відношенню до електричних кіл з лінійним навантаженням, коли характер струму мало відрізняється від синусоїдального, а значить в ньому немає інших значимих за величиною гармонік струму, окрім першої. У таких електричних колах фактичне значення IN струму в N-провіднику, дійсно, залежить тільки від величини 25 несиметрії фазних струмів Iф, а величина I / визначається геометричною сумою фазних струмів N Iф. Проте, в електричних колах з нелінійним навантаженням за наявності у фазних струмах Iф, окрім першої, інших непарних гармонік фактична величина струму в N-провіднику буде визначатися не лише несиметрією фазних струмів, а й величинами струмів третьої гармоніки в фазах. У загальному випадку струм в N-провіднику при нелінійних навантаженнях дорівнюватиме геометричній сумі усіх непарних гармонік струму, не кратних 3, а також арифметичній сумі струмів третьої гармоніки й інших, кратних нею. Таким чином, для побудови таких апаратів та систем захисту електричних кіл 0,4 кВ з Nпровідником, які містять захист від обриву N-провідника, що призводить до можливих перенапруг у однофазних споживачів, необхідно безперервно здійснювати моніторинг гармонійного складу фазних струмів. При цьому слід враховувати, що вказані захисти повинні встановлюватися не в тих апаратах, які захищають конкретні навантаження, у тому числі і нелінійні (випрямлячі, ноутбуки і таке інше), а у ввідних апаратах, через які протікають струми, створені як лінійним, так і нелінійним навантаженням. Кількість значущих за величиною гармонік струму через ввідний захисний апарат не може бути великою. Як правило, у фазних струмах Iф значимими за величиною являються лише перші 3 непарних гармоніки, а саме – 1, 3 та 5-та гармоніки. Тому для побудови зазначених апаратів та систем захистів вважається надмірним використання універсального способу визначення великої кількості вищих гармонік, яким, наприклад, є дискретне перетворення Фур'є [3]. При використанні дискретного перетворення Фур'є (ДПФ) безперервна залежність струму у часі i ф f t i ф t шляхом множення її на ґратчасту дельта-функцію (δ-функцію) 30 35 40 45 50 55 перетворюється в дискретну функцію, за дискретними значеннями i j якої можна визначити величину кожної з гармонік струму. Проте, для розрахунку величин струму будь якої з гармонік потрібно виконати досить велику кількість математичних операцій множення, складання, зведення в квадрат тощо. Головною причиною необхідності проведення великого обсягу математичних операцій при використанні ДПФ є те, що для визначення величини однієї з гармонік струму вимагається провести розрахунок усього ДПФ, тобто усіх гармонік спектру. Таким чином розроблені альтернативні методи дискретного розкладання в ряди Фур'є, які дозволяють визначати фіксовані гармоніки без розрахунку усього спектру. Одним з таких альтернативних методів розкладання в ряди Фур'є є алгоритм Герцеля [4]. Це спеціальна реалізація ДПФ у формі рекурсивного фільтра (фільтр з нескінченною імпульсною характеристикою). У відмінність від швидкого перетворення Фур'є, що обчислює всі частотні 1 UA 102741 C2 5 10 15 компоненти ДПФ, алгоритм Герцеля дозволяє ефективно обчислити значення однієї частотної компоненти. Тому при його використанні спрощується розрахунок спектру гармонік та помітно зменшується кількість необхідних математичних операцій. Проте і широко відомий метод швидкого ДПФ, і альтернативний алгоритм Герцеля, для вирішення окремих завдань є досить витратними за ресурсом для тих мікропроцесорних пристроїв, для яких визначення перших трьох гармонік є не самоціллю, а лише елементом побудови алгоритму захисту електричного кола від тих аварійних ситуацій, які здійснюють вплив на спектральну характеристику струму. Тому вважається доцільним для вирішення окремих випадків визначення діючих значень перших трьох непарних гармонік струму знайти простіший спосіб, що вимагає меншої кількості математичних операцій, а значить вимагає меншого ресурсу мікропроцесора. Найбільш близьким по суті математичних операцій, які використовуються для визначення спектру перших трьох, нижчих, гармонік струму, являється спосіб визначення діючого значення сигналу відповідно до відомої теореми Котельникова [5] і спосіб визначення діючого значення несинусоїдального струму відповідно до регламентації держстандарту з якості електроенергії [6]. Згідно з теоремою Котельникова, якщо безперервний сигнал i ф t має спектр, в якому є n вищих гармонік, обмежений частотою fk, то він може бути однозначно і без втрат відновлений за своїми дискретними відліками i j f t ф , узятими в діапазоні 0 Δt ф 1 . 2fk Теорему Котельникова можна сформулювати зворотним чином. Для того, щоб за дискретними значеннями відновити сигнал на прийомі без втрат (без втрат визначити його діюче значення), необхідно частоту дискретизації fд вибирати строго більшою подвоєної максимальної частоти спектра, тобто більшою за подвоєну частоту fk, k-ї, найбільш високої гармоніки: f д 2fk . 20 25 30 З теореми Котельникова випливають 2 наслідки: - Будь-який аналоговий сигнал може бути відновлений з якою завгодно точністю за своїми дискретними відліками, узятими із частотою , де fk максимальна частота, якою обмежений спектр реального сигналу. - Якщо максимальна частота в сигналі перевищує половину частоти дискретизації, то способу відновити сигнал з дискретного в аналоговий без спотворення не існує. Вимога ж держстандарту з якості електроенергії [6] в частині величини необхідної частоти дискретизації жорсткіша – частота дискретизації fд має бути, як мінімум, в 3 рази більшою за частоту fk, k-ї, найбільш високої гармоніки струму: f д 3fk . (1) 35 40 45 50 55 Вказана розбіжність у вимогах до частоти дискретизації fд пояснюється наступним. Теорема Котельникова розглядає теоретичну можливість (ідеальний випадок) відновлення початкового сигналу за його дискретними значеннями, коли сигнал почався нескінченно давно і ніколи не закінчиться, а також не має в часовій характеристиці точок розриву. Саме це має на увазі поняття "спектр, обмежений частотою fk". Це означає, що для визначення діючого значення сигналу період інтегрування квадратів дискретних значень може виявитись неприпустимо великим. Зрозуміло, що в реальних випадках вказаний діапазон інтегрування має бути мінімізований. Наприклад, якщо як сигнал мати аналогову залежність зміни несинусоїдального фазного струму від часу i ф f t , то максимальним діапазоном інтегрування буде період зміни струму першої основної гармоніки T1. Для такого, порівняно невеликого інтервалу інтегрування, вимоги до частоти дискретизації мають бути жорсткішими, що й відображено в держстандарті з якості електроенергії [6]. З урахуванням вищевикладеного теоретичного підґрунтя, найбільш близьким по суті математичних операцій, які використовуються для визначення спектра перших трьох, нижчих, гармонік струму, є спосіб визначення діючого значення струму, що регламентується держстандартом [6]. Згідно з цим способом визначення діючого значення несинусоїдального струму необхідно здійснювати методом чисельного інтегрування квадратів миттєвих значень струму за період часу, не менший за час одного періоду зміни струму першої основної гармоніки. При цьому мінімальна необхідна кількість таких миттєвих значень струму синусоїди найвищої k-ї гармоніки з частотою, що дорівнює k f1 , має бути не менше трьох за її період, де f1 – частота першої гармоніки. 2 UA 102741 C2 Це означає, що співвідношення частоти дискретизації вимірювань миттєвих значень струму fд з частотою fk найбільш високої k-ї гармоніки визначається наступним виразом: f д 3k f1 . 5 (2) Для реалізації чисельного інтегрування необхідно безперервну функцію залежності струму від часу i ф f t перетворити в дискретну, причому з визначеною частотою дискретизації. Для цього здійснюють множення залежності i ф f t на ґратчасту δ-функцію δt , вираз якої має наступний вигляд: t t nt n , (3) 10 15 де t n – часовий інтервал дискретизації δ-функції; n – число часових інтервалів t n в періоді зміни струму першої гармоніки T1 . Діюче значення несинусоїдального струму визначається методом чисельного інтегрування квадратів миттєвих значень струму, які відповідають дискретним значенням результату множення залежності зміни струму в часі i ф f t на ґратчасту δ-функцію t nt n . Інтегрування здійснюють в діапазоні часу від 0 до значення, що дорівнює періоду зміни струму першої гармоніки T1 . Щоб задовольнити вимогу (1) з частоти дискретизації, значення часового інтервалу дискретизації ґратчастої δ-функції вибирають за умови: t n 1 Tn , 3 (4) 20 25 де Tn – період зміни струму n-ї гармоніки. Розглянутий спосіб дозволяє з необхідною точністю обчислити діюче значення струму при наявності в ньому визначеної кількості n вищих гармонік струму. При цьому необхідна точність урахування усіх n гармонік забезпечується за рахунок того, що при перетворенні безперервної залежності фазного струму від часу i ф f t в дискретну, вказана залежність множиться на 30 ґратчасту δ-функцію зі значенням інтервалу дискретизації t n , як мінімум, у три рази меншим, ніж період найбільш високої k-ї гармоніки. Проте розглянутий спосіб визначення діючого значення струму не дозволяє визначати величину кожної з n гармонік, сума яких і формує початкову залежність несинусоїдального фазного струму від часу i ф f t . 35 40 В основу винаходу поставлена задача розробити такий спосіб визначення діючого значення Iф несинусоїдального фазного струму i ф f t , який за рахунок вибору додаткових значень часового інтервалу дискретизації ґратчастої δ-функцію, дозволяє: - визначити не лише діюче значення суми усіх гармонік струму, але і значення діючих значень струмів кожної з n гармонік; - істотно знизити необхідну кількість математичних операцій для визначення діючих значень струмів перших трьох непарних гармонік (величини саме цих гармонік в електромережах 0,4 кВ є найбільш значущими). Поставлена задача вирішується в способі визначення діючих значень періодичного несинусоїдального струму i його непарних гармонік шляхом множення залежностей струму від часу на ґратчасту дельта-функцію з різними інтервалами дискретизації, у якому параметри електричного кола необхідні для побудови апаратів та систем релейно-струмового захисту мереж електропостачання, а саме діюче значення несинусоїдального фазного струму Iф визначають методом чисельного інтегрування, в діапазоні часу від 0 до значення, що дорівнює 45 періоду зміни струму першої гармоніки Т1, квадратів тих миттєвих значень струму i2 , які j відповідають дискретним значенням результату множення залежності зміни струму в часі i ф f t на ґратчасту δ-функцію t t ф , де інтервал дискретизації Δt ф ґратчастої функції в 3 і більше разів менший за період Tk зміни струму найвищої k-ї непарної гармоніки струму 3 UA 102741 C2 3Δt ф Tk , за рахунок того, що розчіплювач апарата захисту додатково містить вузол, в якому додатково здійснюють множення залежності зміни струму в часі i ф f t на ґратчасту δ 5 функцію t nt n , при цьому інтервал дискретизації ґратчастої δ-функції Δtn в 2 рази менший за період зміни струму n-ї гармоніки, де n k, k 2 , k 4 , 1 – номер непарної гармоніки, після чого методом чисельного інтегрування квадратів тих миттєвих значень струму, які відповідають дискретним значенням результату множення залежності зміни струму в часі i ф f t на ґратчасту δ-функцію t kt k , визначають діюче значення струму без урахування найбільшої k-ї гармоніки, тобто струму Iфk 2 , в якому найвищою є k 2 гармоніка, після чого 10 визначають діюче значення струму k-ї гармоніки Ik з виразу Ik I2 I2 , потім, для ф ф k 2 визначення діючого значення наступної більш низької, k 2 -ї гармоніки струму Iф , роблять множення залежності від часу струму k-ї гармоніки, що виражається залежністю ik f t Ikmsinkt , на ґратчасту δ-функцію t k 2t k 2 , після чого отримані дискретні значення струму k-ї гармоніки i jk Ik sinkjt k 2 віднімають з миттєвих значень струму i jфk 2 , які відповідають дискретним значенням результату множення залежності зміни струму у часі 15 i ф f t на ґратчасту δ-функцію t k 2t k 2 , потім отримані миттєві значення струму i jk 4 i jфk 2 i jk зводять в квадрат і методом їх чисельного інтегрування отримують діюче значення струму Iфk 4 , в якому найвищою є k 4 гармоніка, після чого визначають діюче значення струму k 2 -ї з виразу Ik 2 I2 I2 I2 , після цього ф k ф k 4 аналогічним методом визначають діюче значення наступних, нижчих гармонік з виразу 20 2 Iфn Iф гармоніки Ik 2 k 2 2 Ip Iфn 1 . p n 1 Саме, за рахунок того, що розчіплювач апарата захисту додатково містить вузол, в якому додатково здійснюють множення залежності зміни струму в часі i ф f t на ґратчасту δ-функцію 25 t nt n , при цьому інтервал дискретизації ґратчастої δ-функції Δtn в 2 рази менший за період зміни струму n-ї гармоніки, де n k, k 2 , k 4 , 1 – номер непарної гармоніки, після чого методом чисельного інтегрування квадратів тих миттєвих значень струму, які відповідають дискретним значенням результату множення залежності зміни струму в часі i ф f t на ґратчасту δ-функцію t kt k , визначають діюче значення струму без урахування найбільшої k-ї гармоніки, тобто струму Iфk 2 , в якому найвищою є k 2 гармоніка, після чого визначають 30 діюче значення струму k-ї гармоніки Ik з виразу Ik I2 I2 , потім, для визначення ф ф k 2 діючого значення наступної більш низької, k 2 -ї гармоніки струму Iф , роблять множення залежності від часу струму k-ї гармоніки, що виражається залежністю ik f t Ikmsinkt , на ґратчасту δ-функцію t k 2t , після чого отримані дискретні значення струму k-ї k2 гармоніки i jk Ik sinkjt k 2 віднімають з миттєвих значень струму i jфk 2 , які відповідають дискретним значенням результату множення залежності зміни струму у часі i ф f t на 35 ґратчасту i jk 4 i jфk 2 i jk t k 2t k 2 , потім отримані миттєві значення струму зводять в квадрат і методом їх чисельного інтегрування отримують діюче δ-функцію значення струму Iфk 4 , в якому найвищою є k 4 гармоніка, після чого визначають діюче k 2 -ї з виразу Ik 2 I2 I2 I2 , після цього ф k ф k 4 аналогічним методом визначають діюче значення наступних, нижчих гармонік з виразу значення струму гармоніки Ik 2 4 UA 102741 C2 2 Iфn Iф k 2 2 Ip Iфn 1 , забезпечується визначення не лише діючого значення суми усіх p n 1 гармонік струму Iф, але і діючих значень струмів Iфn кожної з n гармонік. 5 10 15 20 Дійсно, адже визначення діючих значень Iфn кожної з n гармонік за рахунок вибору інтервалу дискретизації Δtn , що дорівнює половині періоду зміни струму шуканої n-ї гармоніки, засновано на теоремі Котельникова, а точніше на наслідках з цієї теореми. З теореми Котельникова випливають 2 наслідки [5]: 1. Будь-який аналоговий сигнал може бути відновлений з якою завгодно точністю за своїми дискретними відліками, узятими із частотою , де fk максимальна частота, якою обмежений спектр реального сигналу. 2. Якщо максимальна частота в сигналі перевищує половину частоти дискретизації , то способу відновити сигнал з дискретного в аналоговий без спотворення не існує. До вказаних двох наслідків з теореми Котельникова додамо третій наслідок, який сформулюємо наступним чином: 3. Якщо максимальна частота в сигналі дорівнює половині частоти дискретизації , тобто , а початок відліку відповідає дискретному значенню, рівному нулю, то спотворення аналогового сигналу при відновленні з дискретного дорівнюватиме величині сигналу найбільш високої k-ї гармоніки. Цілком очевидно, що при одночасному використанні першого і третього наслідків теореми Котельникова досить просто можна визначити величину найвищою гармоніки, а потім і більш низьких. Якщо під сигналом розуміти залежність струму електричного кола в часі i ф f t , то одночасне використання зазначених наслідків з теореми Котельникова полягає в тому, що аналогова залежність i ф f t множиться на гратчасті δ-функції як з частотами дискретизації f д більшими, ніж подвоєна частота найбільшої гармоніки струму fk ( f д 2fk ), так і з частотою 25 30 дискретизації, що дорівнює подвійній частоті тієї ж гармоніки ( f д 2fk ). Суть способу визначення діючих значень періодичного несинусоїдального струму i його непарних гармонік шляхом множення залежностей струму від часу на ґратчасту дельта-функцію з різними інтервалами дискретизації, що заявляється, пояснюється кресленнями фіг. 1÷3. На фіг. 1 наведені діаграми, що ілюструють суть множення аналогової залежності струму від часу i ф f t на ґратчасту δ-функцію t t . ф На фіг. 2 наведені діаграми, що ілюструють суть визначення спектра гармонік несинусоїдального струму, шляхом множення залежності струму від часу i ф f t на ґратчасту δ-функцію з частотою дискретизації f д , що дорівнює подвійній частоті шуканої гармоніки fn ( f д 2fn ). 35 На фіг. 3 наведений алгоритм роботи мікропроцесорного розчіплювача автоматичного вимикача, або іншого мікропроцесорного пристрою захисту (ПЗМ), при реалізації способу визначення спектру непарних гармонік струму у фазі. Як видно з діаграм (фіг. 1), геометричною інтерпретацією множення залежності струму від часу i ф f t на ґратчасту δ-функцію t t є визначення крапок перетину часових відліків ф 40 δ-функції з кривої залежності i ф f t . Сукупність вказаних крапок перетину і є дискретною залежністю струму від часу i фд f t . Саме за цими дискретними значеннями струму i j методом чисельного інтегрування квадратів означених значень Z i 2 Δt ф j визначають діючі 1 значення струму у фазах Iф і діючі значення струмів складових гармонік Iфn . Очевидно, що 45 якщо точки перетину часових відліків δ-функції з кривою залежності струму n-ї гармоніки завжди припадатимуть на момент проходження струму через нуль (у разі f д 2fn ), то значення струму цієї гармоніки i jn не буде враховано при обчисленні діючого значення фазного струму Iф. Це 5 UA 102741 C2 дозволяє шляхом послідовного виключення струму i jn кожної n гармоніки при обчисленні сумарного діючого значення струму у фазі Iф визначити значення струму кожної гармоніки. На фіг. 2 наведені діаграми, що ілюструють суть визначення гармонічного складу струму Iф за рахунок множення аналогової залежності фазного струму i ф f t на ґратчасту δ-функцію з 5 різними інтервалами дискретизації t n або, що те ж саме, з різною частотою дискретизації. На фіг. 2,а наведені криві залежностей від часу струмів 1, 3 та 5 гармонік струму, а також залежність від часу фазного струму i ф f t , що є сумою залежностей від часу фазних струмів усіх гармонік. Ґратчаста δ-функція, на яку множаться часові залежності i1 f t , i 3 f t , i 5 f t , має інтервал дискретизації t n , щонайменш втричі менший періоду найбільш високої 10 5-ї гармоніки струму (тобто частота дискретизації f д 3f5 ). 1 T5 ) діючі значення усіх 3 гармонік струму Iф визначають без спотворень, з урахуванням значення струму 5-ї гармоніки I5 . Для наочності на фіг. 2,а фазний струм Iф представлено у вигляді коаксіальних трубок, перерізи яких відповідають величинам струмів різних гармонік, а переріз провідника відповідає величині фазного струму Iф. Математична залежність, що пов'язує величину фазного струму Iф та величини струмів 1, 3 та 5-ї гармоніки, визначається виразом: При такому інтервалі дискретизації ґратчастої δ-функції ( t n 15 2 2 2 Iф I1 I3 I5 . 20 (5) На фіг. 2,б, як і на фіг. 2,а, наведені криві залежностей від часу струмів 1, 3 та 5-ї гармоніки струму. Але ґратчаста δ-функція, на яку множаться залежності i1 f t , i 3 f t , i 5 f t , має інтервал дискретизації t д , що дорівнює половині періоду найвищої, 5-ї гармоніки струму 1 T5 (тобто частота дискретизації f д 2f5 ). В цьому випадку точки перетину часових 2 відліків δ-функції із залежністю струму 5-і гармоніки від часу i 5 f t завжди відповідатимуть моменту переходу струму цієї гармоніки через нуль, а це означає, що ця гармоніка струму не буде врахована. Тому, при інтервалі дискретизації ґратчастої δ-функції, що дорівнює половині періоду зміни 1 струму 5-ї гармоніки t д5 T5 , знайдене діюче значення струму у фазі Iф - 5 складатиметься 2 тільки з двох гармонік – 1 та 3-ї, а 5-ї гармоніки в ньому не буде. Тому на фіг. 2,б в перерізі провідника показані тільки дві коаксіальні трубки із струмами 1 та 3-ї гармоніки – I1 та I3 . t д5 25 30 Математична залежність, що пов'язує величину фазного струму Iф - 5 із величинами струмів 1 та 3-ї гармоніки, визначається виразом: 2 2 Iф - 5 I1 I3 . 35 З урахуванням виразів (5) та (6) величину струму 5-ї гармоніки визначається з наступного виразу: 2 2 I5 Iф Iф 5 . 40 (6) (7) На фіг. 2,в наведені криві залежностей від часу струмів 1, 3 і 5-ї гармоніки струму. Але ґратчаста δ-функція, на яку множаться залежності i1 f t , i 3 f t , i 5 f t , має інтервал дискретизації t д , що дорівнює половині періоду 3-ї гармоніки струму t д3 6 1 T3 (тобто 2 UA 102741 C2 5 частота дискретизації f д 2f3 ). В цьому випадку точки перетину часових відліків δ-функції із залежністю від часу струму 3-ї гармоніки i 3 f t завжди відповідатимуть моменту переходу струму цієї гармоніки через нуль, а це означає, що при обчисленні діючого значення фазного струму 3-я гармоніка струму не буде врахована. Тому знайдене значення фазного струму може бути позначене як Iф - 3 . 1 T3 перетинатимуть 2 залежність струму 5-ї гармоніки від часу i 5 f t в моменти часу, коли миттєві значення струму цієї гармоніки i j5 не дорівнюватимуть нулю. Тому, щоб запобігти впливу струму 5-ї гармоніки Проте часові відліки δ-функції з інтервалом дискретизації t д3 10 при визначенні струму 3-ї гармоніки, зі значень струму, що відповідають точкам перетину дискретних відліків із залежністю струму i ф f t , віднімають відповідні значення i j5 I5m sin5jt д3 . В цьому випадку знайдене діюче значення струму у фазі, яке може бути позначене як I ф-3-5 , складатиметься тільки зі струму 1-ї гармоніки, тобто Iф-3-5 I1 . Величину струму 3-ї гармоніки I3 визначають з виразу: 2 2 2 I3 Iф I5 I1 . (8) 15 20 25 Блок-схема, що ілюструє алгоритм роботи мікропроцесорного розчіплювача автоматичного вимикача, або іншого ПЗМ, при реалізації запропонованого способу визначення діючих значень періодичного несинусоїдального струму i його непарних гармонік шляхом множення залежностей струму від часу на ґратчасту дельта-функцію з різними інтервалами дискретизації, наведена на фіг. 3. Окремі обчислювальні і логічні операції, які робить мікропроцесорний пристрій, на фіг. 3 умовно позначені у вигляді модулів. Фізично вказані модулі не існують, їх зображення потрібне для зручності викладу функціонування мікропроцесорного пристрою при реалізації запропонованого способу визначення спектра гармонік фазного струму. Функціонує мікропроцесорний пристрій, при реалізації запропонованого способу визначення спектру гармонік фазного струму, таким чином: 1. У модулі 1 за допомогою датчиків струму (ДС) формується аналогова залежність фазного струму від часу i ф f t . 2. У модулі 2 здійснюють множення аналогової залежності струму у фазі від часу i ф f t на ґратчасту δ-функцію t t з часовим інтервалом дискретизації t ф , як мінімум, в 3 рази ф 30 менший, ніж період найвищої з гармонік, величина якої є значущою. У конкретному випадку такою, значущою за величиною (більше 5 % величини струму у фазі Iф ), прийнята 5-та гармоніка фазного струму, тому величина інтервалу дискретизації ґратчастої δ-функції 1 відповідає нерівності: t ф T5 . 3 3. У модулі 3 визначають дискретні значення i j фазного струму i фд f t , як результат 35 множення аналогового сигналу від датчика струму i ф f t на гратчасту δ-функцію з часовим інтервалом дискретизації t ф . 4. У модулі 4 методом чисельного інтегрування квадратів дискретних значень i j струму Z i ф f t визначають діюче значення фазного струму Iф з виразу: Iф i 2 Δt ф j T , де Z 1 . T1 t ф 5. У модулі 5 здійснюють множення аналогової залежності фазного струму i ф f t на 40 1 ґратчасту δ-функцію з часовим інтервалом дискретизації t д , що дорівнює половині періоду 1 найвищої, 5-ї гармоніки фазного струму t д5 T5 . 2 7 UA 102741 C2 6. У модулі 6 визначають дискретні значення i jф-5 фазного струму без урахування 5-ї гармоніки, як результат множення аналогового сигналу від датчика струму i ф f t на ґратчасту 5 δ-функцію з часовим інтервалом дискретизації t д5 . 7. У модулі 7 методом чисельного інтегрування квадратів дискретних значень струму i ф-5 f t визначають діюче значення струму у фазі без урахування струму 5-ї гармоніки Iф - 5 з Z виразу: Iф - 5 i 2ф - 5 Δt д5 j 1 T1 , де Z T1 . t д5 8. У модулі 8 визначають діюче значення струму 5-ї гармоніки з виразу I5 I2 I2 . ф ф5 9. У модулі 9 здійснюють множення аналогової залежності фазного від часу i ф f t на 10 ґратчасту δ-функцію з часовим інтервалом дискретизації t д , що дорівнює половині періоду 3-ї 1 гармоніки фазного струму t д3 T3 . 2 10. У модулі 10 визначають дискретні значення i jф-3 фазного струму без урахування 3-ї гармоніки, як результат множення аналогового сигналу від датчика струму i ф f t на ґратчасту δ-функцію з часовим інтервалом дискретизації t д3 . 11. У модулі 11 визначають дискретні значення i j5 залежності струму 5-ї гармоніки від часу 15 i 5 f t , як результат множення аналогової залежності струму цієї гармоніки від часу i5 I5msin5t на ґратчасту δ-функцію з часовим інтервалом дискретизації t д3 . 12. У модулі 12 визначають дискретні значення i jф-3-5 фазного струму без урахування 5-ї та 3-ї гармоніки, як різницю дискретних значень фазного струму без урахування 3-ї гармоніки i jф-3 , що отримується з модуля 10, та дискретних значень струму 5-ї гармоніки, що 20 отримується з модуля 11: i jф- 3- 5 i jф- 3 i j5 . 13. У модулі 13 визначають діюче значення струму у фазі без урахування струмів 3-ї та 5-ї гармонік, яке дорівнює діючому значенню струму першої гармоніки, з виразу: Z Iф - 5 - 3 14. 25 I3 2 Iф i2ф- 5- 3 Δt д3 j 1 T1 У модулі 2 I5 2 Iф 5 3 I1 , де Z 14 T1 . t д3 визначають діюче значення струм 3-ї гармоніки з виразу . Наведена блок-схема роботи мікропроцесорного пристрою при визначенні діючих значень як повного несинусоїдального струму у фазі Iф , так і перших трьох непарних гармонік (1, 3 та 5 30 35 ї) дозволяє визначити необхідну для цього кількість математичних операцій. Так, якщо припустити, що дискретні значення фазного струму відомі, то кількість необхідних математичних операцій можна оцінювати тільки по операціях саме з цими вже відомими дискретними значеннями i j фазного струму iф f t . Якщо прийняти, що для надійного визначення перших трьох непарних гармонік струму, включаючи 5-ту, часовий інтервал 1 дискретизації вибрати таким, що дорівнює періоду 5-ї гармоніки, то кількість необхідних 3 математичних операцій визначення гармонічного спектру фазного струму становить – 61. При використанні дискретного перетворення Фур'є, для визначення спектра перших трьох непарних гармонік (1, 3 та 5-ї), необхідно для кожної з гармонік взяти мінімум 30 відомих дискретних значень i j фазного струму. Як показує аналіз, для цього необхідно зробити 453 різних математичних операції (складання, віднімання, зведення в квадрат, добування кореня тощо), що, приблизно, в 7,5 разу більше, ніж в заявленому способі (61 операція). 8 UA 102741 C2 5 10 15 20 25 30 При використанні алгоритму Герцеля, який є одним з альтернативних методів розкладання в ряди Фур'є у формі рекурсивного фільтра (фільтр з нескінченною імпульсною характеристикою), кількість математичних операцій для знаходження значення однієї гармоніки виходить значно меншою. Так, наприклад, як показує аналіз, для розрахунку величини однієї гармоніки потрібно 71 операцію, а для трьох гармонік (1, 3 і 5) – 273 операції, що в 4,8 раз більше, ніж в заявленому способі. З приведених вище результатів порівняльного аналізу витікає, що при використанні запропонованого способу визначення діючих значень періодичного несинусоїдального струму i його непарних гармонік шляхом множення залежностей струму від часу на ґратчасту дельтафункцію з різними інтервалами дискретизації кількість необхідних для цього математичних операцій виходить значно меншою. Таким чином, поставлене при розробці цього способу завдання визначення діючих значень не тільки повного несинусоїдального струму, як того потребує ГОСТ 13109-97 [6], а і його перших трьох непарних гармонік, виконано. Також реалізована і мета по істотному зниженню необхідних для цього математичних операцій, порівняно з існуючими методами. Джерела інформації: 1. Пат. 81981 України МПК H 02 H 7/00, H 01 H 73/00 Система захисту розгалужених трифазних електричних кіл від струмів віддалених коротких замикань / Г.М. Гапоненко, В.В. Омельченко, О.С. Кобозєв. – №a200604596. Заявлено 25.04.2006; Опубл. 25.02.2008, Бюл. №4. 2. Сосков А.Г, Кобозев А.С. Модернизация системы защиты городских электрических сетей 0,4 кВ за счет использования микропроцессорной техники в расцепителях выключателей / Свiтлотехнiка та електроенергетика.-2010. – №2. – С. 53-63. 3. Сергиенко А.Б. Цифровая обработка сигналов: Учебник для вузов. 2-е изд. – СПб.: Питер, 2006.-751 с. 4. Блейхут Р. Быстрые алгоритмы цифровой обработки сигналов: Пер. с англ. – М.: Мир, 1989.-448 с. 5. Басараб М.А., Зелкин Е.Г., Кравченко В.Ф., Яковлев В.П. Цифровая обработка сигналов на основе теоремы Уиттекера-Котельникова-Шеннона. – М.: Радиотехника, 2004.-72 с. 6. ГОСТ 13109-97. Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения. ФОРМУЛА ВИНАХОДУ 35 40 Спосіб визначення діючих значень періодичного несинусоїдального струму i його непарних гармонік шляхом множення залежностей струму в часі на ґратчасту дельта-функцію з різними інтервалами дискретизації за допомогою модулів мікропроцесора апарата захисту електричних кіл, у якому параметри електричного кола, необхідні для побудови апаратів та систем релейно-струмового захисту мереж електропостачання, а саме діюче значення несинусоїдального фазного струму Iф , визначають методом чисельного інтегрування, в діапазоні часу від 0 до значення, що дорівнює періоду зміни струму першої гармоніки T1 , квадратів тих миттєвих значень фазного струму i2 , отриманих з датчиків струму, що j відповідають дискретним значенням результату множення залежності зміни фазного струму в часі iф f t на ґратчасту δ-функцію t t ф , де інтервал дискретизації Δt ф ґратчастої 45 функції в три і більше разів менший за період Tk зміни струму найвищої k-ї непарної гармоніки струму 3Δt ф Tk , який відрізняється тим, що в апараті захисту додатково застосовують поєднаний з датчиками струмів мікропроцесорний розчіплювач, в якому здійснюють множення залежності зміни фазного струму в часі iф f t на ґратчасту δ-функцію t ntn , при цьому інтервал дискретизації ґратчастої δ-функції Δtn в два рази менший за період зміни струму n-ї 50 гармоніки, де n k, k 2 , k 4 , 1 - номер непарної гармоніки, після чого методом чисельного інтегрування квадратів тих миттєвих значень струму, які відповідають дискретним значенням результату множення залежності зміни фазного струму в часі iф f t на ґратчасту δ-функцію t ktk , визначають діюче значення струму без урахування найбільшої k-ї гармоніки, тобто струму Iфk 2 , в якому найвищою є k 2 гармоніка, після чого визначають 9 UA 102741 C2 2 2 діюче значення струму k-ї гармоніки Ik з виразу Ik Iф Iфk 2 , потім, для визначення діючого k 2 -ї значення наступної більш низької, гармоніки струму Iф , здійснюють множення залежності від часу струму k-ї гармоніки, що виражається залежністю ik f t Ikmsinkt , на ґратчасту δ-функцію t k 2tk 2 , після чого отримані дискретні значення струму k-ї 5 10 гармоніки i jk Iksinkjtk 2 віднімають з миттєвих значень струму i jфk 2 , які відповідають дискретним значенням результату множення залежності зміни фазного струму у часі iф f t на t k 2tk 2 , ґратчасту δ-функцію потім отримані миттєві значення струму i j k 4 i jфk 2 i jk зводять в квадрат і методом їх чисельного інтегрування отримують діюче значення струму Iфk 4 , в якому найвищою є k 4 гармоніка, після чого визначають 2 2 2 діюче значення струму k 2 -ї гармоніки Ik 2 з виразу Ik 2 Iф Ik Iфk 4 , після цього аналогічним методом визначають діюче значення наступних, нижчих гармонік з виразу 2 Iфn Iф k 2 2 Ip Iфn1 . p n1 10 UA 102741 C2 11 UA 102741 C2 12 UA 102741 C2 Комп’ютерна верстка Д. Шеверун Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 13
ДивитисяДодаткова інформація
Назва патенту англійськоюMethod for determination of root-mean-square of periodic nonsinusoidal current and odd harmonics thereof via multiplication of current-time dependence and lattice delta function with different quantization intervals
Автори англійськоюKoboziev Oleksandr Serhiiovych, Sereda Oleksandr Hryhorovych
Назва патенту російськоюСпособ определения действующих значений периодического несинусоидального тока и его нечетных гармоник путем умножения зависимостей тока от времени на решетчатую дельта-функцию с разными интервалами дискретизации
Автори російськоюКобозев Александр Сергеевич, Середа Александр Григорьевич
МПК / Мітки
МПК: H02H 7/00, H01H 73/00, H02H 3/08
Мітки: дискретизації, визначення, періодичного, шляхом, інтервалами, часу, несинусоїдального, різними, спосіб, гратчасту, залежностей, множення, непарних, струму, гармонік, значень, дельта-функцію, діючих
Код посилання
<a href="https://ua.patents.su/15-102741-sposib-viznachennya-diyuchikh-znachen-periodichnogo-nesinusodalnogo-strumu-i-jjogo-neparnikh-garmonik-shlyakhom-mnozhennya-zalezhnostejj-strumu-vid-chasu-na-gratchastu-delta-funkci.html" target="_blank" rel="follow" title="База патентів України">Спосіб визначення діючих значень періодичного несинусоїдального струму і його непарних гармонік шляхом множення залежностей струму від часу на гратчасту дельта-функцію з різними інтервалами дискретизації</a>
Попередній патент: Прес поршневий
Наступний патент: Спосіб одержання композитного матеріалу-перетворювача енергії поля
Випадковий патент: Автомобільний вітрогенератор