Спосіб визначення локальних деформацій кристалів на основі профілів розподілу інтенсивності зворотно відбивних електронів

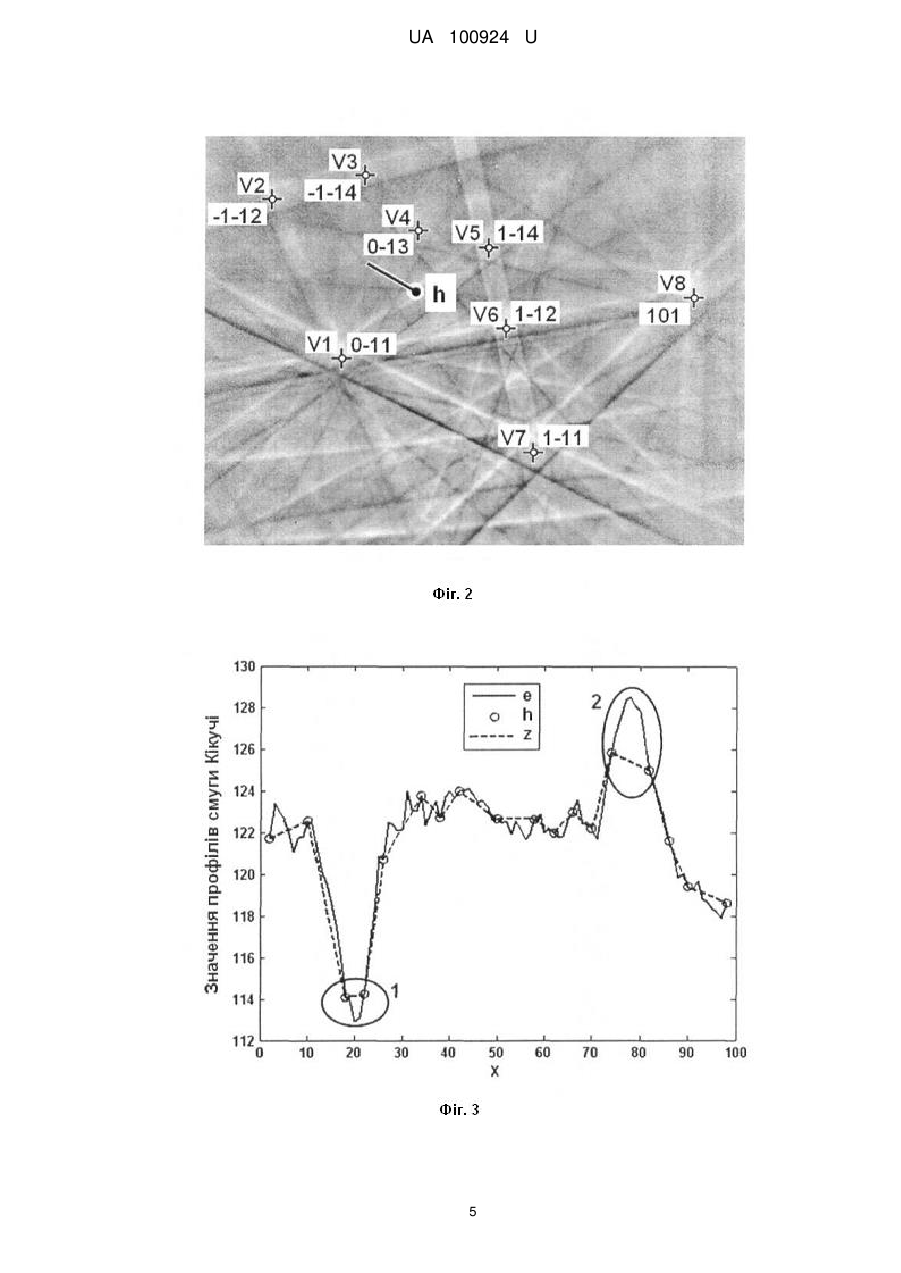
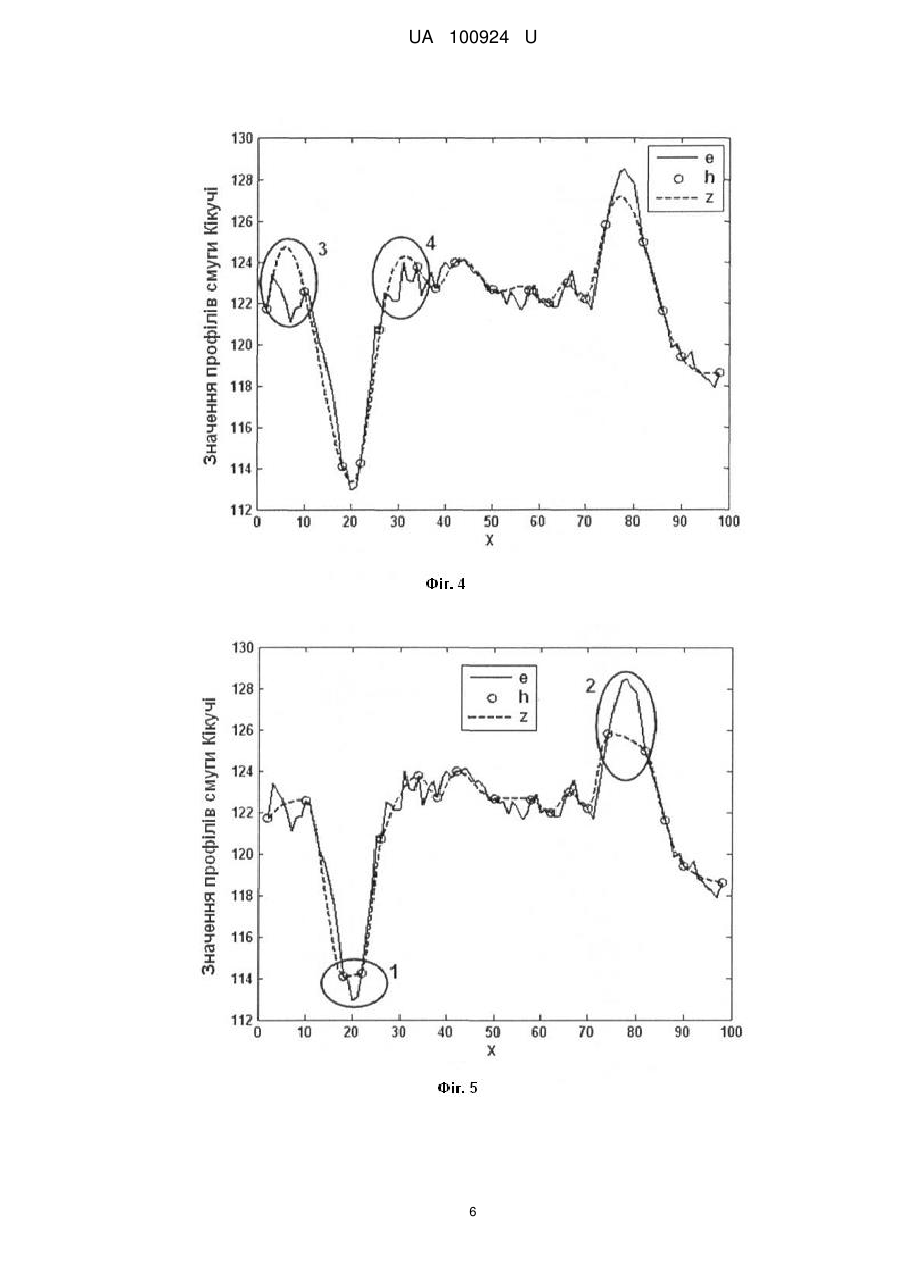
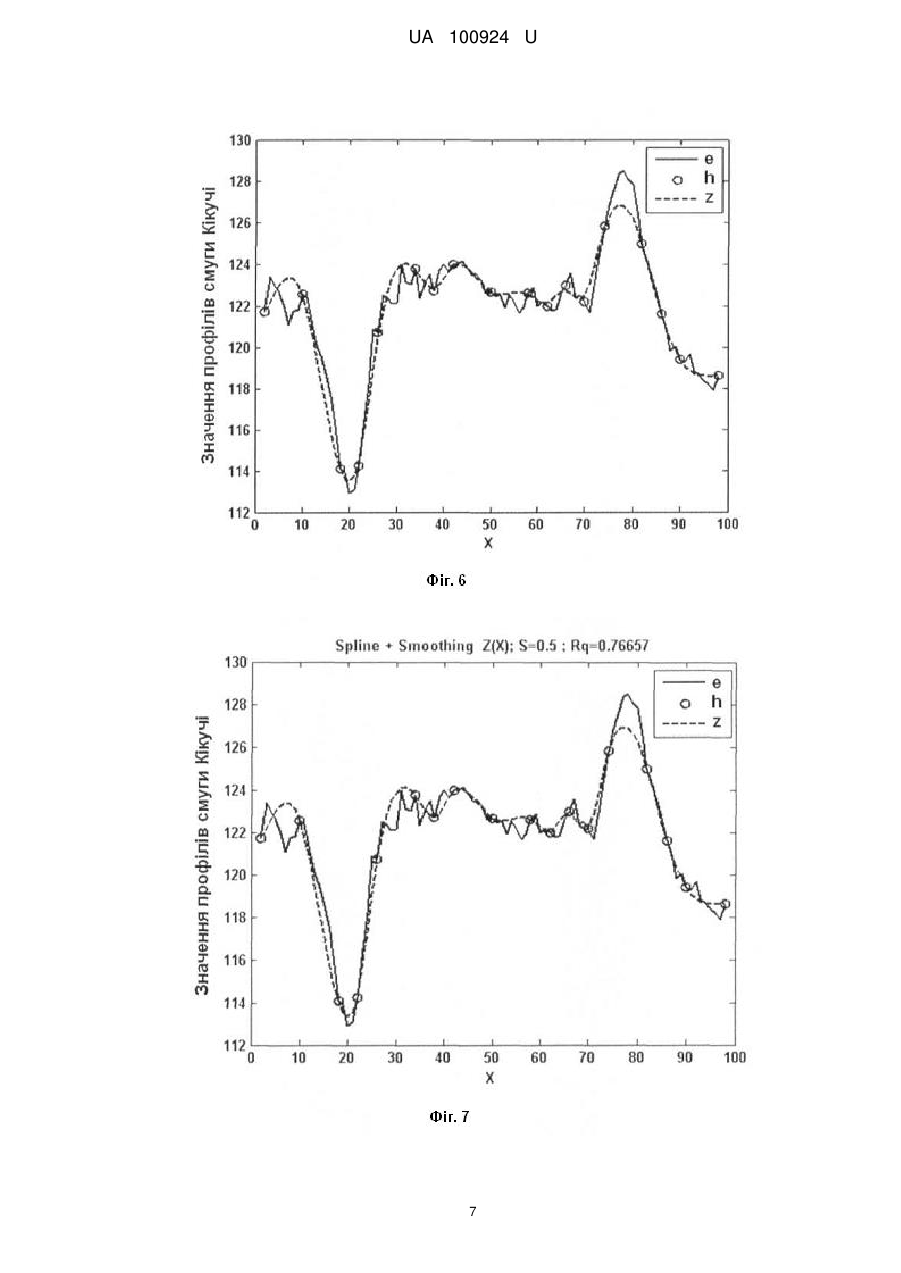
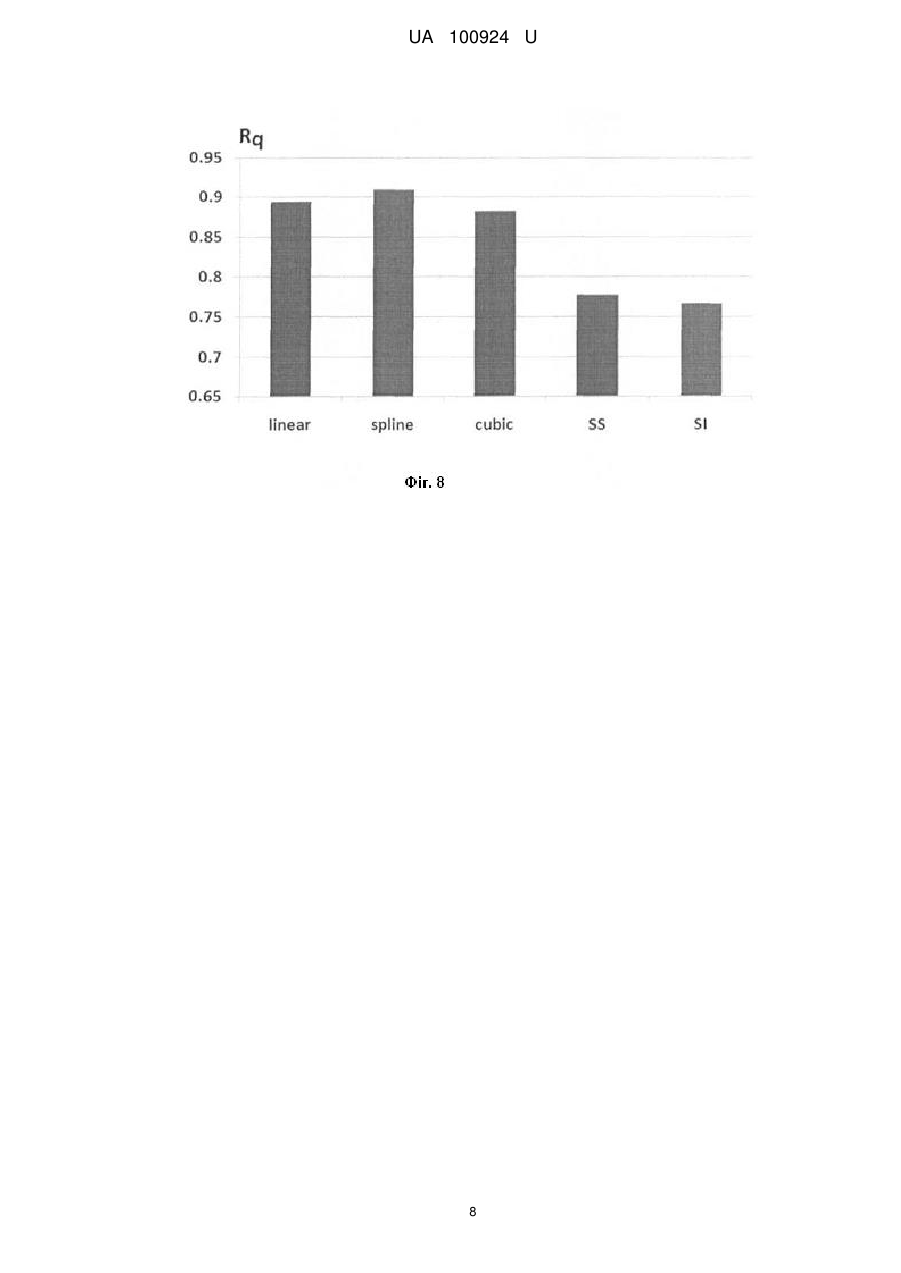
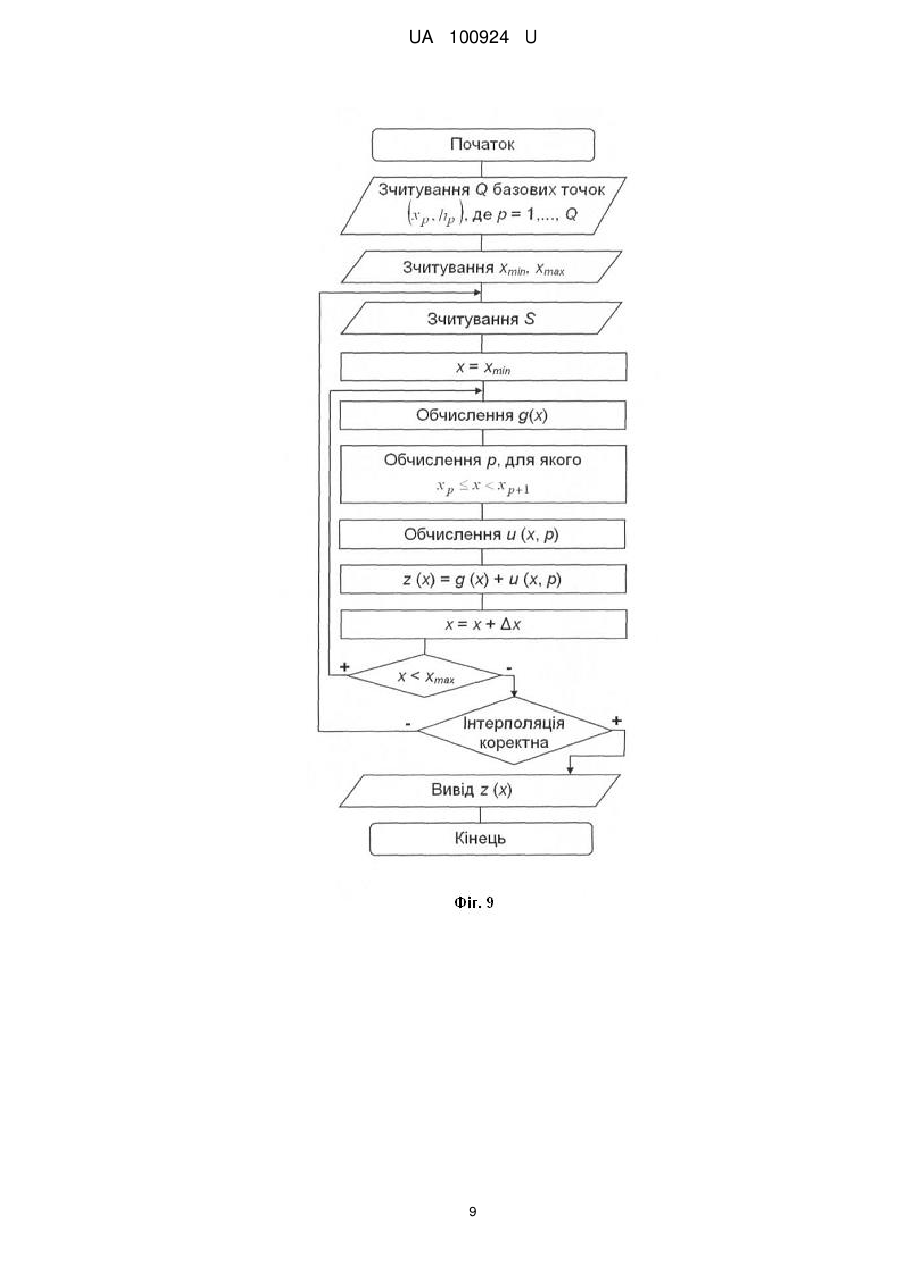
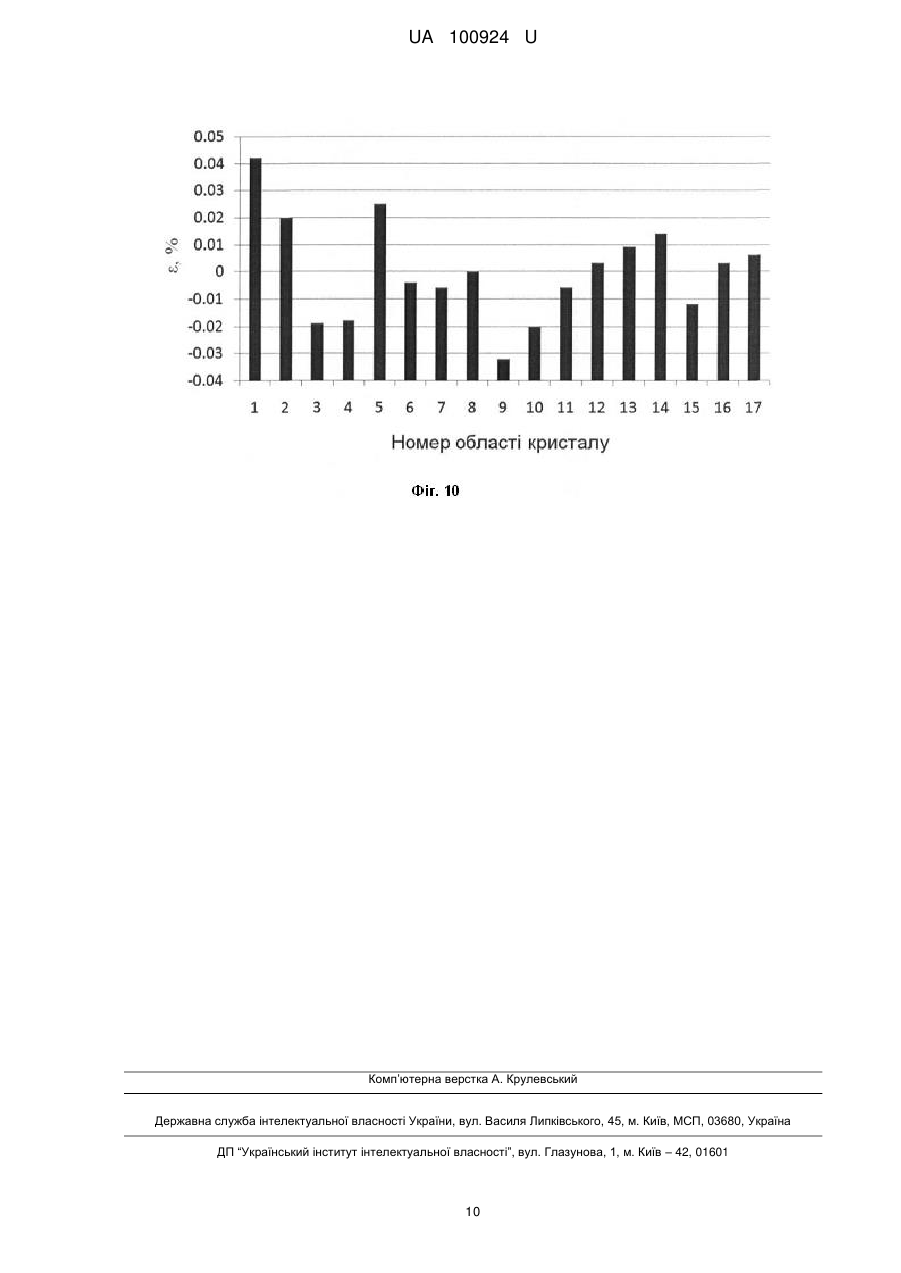
Реферат: Спосіб визначення локальних деформацій кристалів на основі профілів розподілу інтенсивності зворотно відбитих електронів, отримані за методом Кікучі в множині областей кристалу, який полягає в тому, що для кожної області кристалу значення локальної деформації обчислюють через площу під інтерпольованим профілем z(х) смуги Кікучі, отриманої в скануючому електронному мікроскопі від відповідної області досліджуваного кристалу. Значення профілю z(х) отримують шляхом інтерполяції експериментального профілю h(х), заданого в Q базових точках з координатами (хр, hp), де номер точки р=1,…, Q. Для всіх областей кристалу встановлюють однакову відстань від досліджуваної області на кристалі до CCD детектора скануючого електронного мікроскопа. Значення інтерпольованого профілю z(x) обчислюють як суму згладженої функції g (x), яка апроксимує базові точки, та лінійної узгоджуючої функції u(х,р), яка плавно наближує значення функції z(x) до hp у вузлах інтерполяції р, де як функцію g(x) використовують згладжуючі сплайни (Smoothing Spline) з адаптивним згладжуванням. UA 100924 U (12) UA 100924 U UA 100924 U 5 10 15 20 25 30 35 40 45 50 55 60 Корисна модель належить до неруйнівної діагностики структурних порушень у кристалах за даними електронно-дифракційних методів, зокрема методу Кікучі, і може бути практично використана для отримання і обробки профілю розподілу інтенсивності зворотно відбитих електронів з метою більш точного визначення просторового розподілу деформацій досліджуваних кристалів [1-4]. Метод дифракції зворотно відбитих електронів (EBSD-Electron backscatter diffraction), відомий як метод Кікучі, використовується для визначення розмірів і орієнтації кристалів, а також для визначення просторового розподілу деформацій в монокристалах і полікристалічних плівках [1-2]. Даний метод реалізується в скануючому електронному мікроскопі, в якому двовимірна дифракційна картина (картина Кікучі) від локальної області зразка реєструється CCD камерою у вигляді цифрового зображення, а пучок електронів падає на поверхню кристалу під кутом 70°. Картина Кікучі складається з набору смуг Кікучі, а кожна смуга - з двох ліній Кікучі (темної та світлої). Одновимірний розподіл інтенсивності дифракційної картини вздовж напряму, перпендикулярному до смуги Кікучі, називається профілем смуги Кікучі. Аналіз профілю смуги Кікучі, який має яскраво виражені мінімум і максимум, використовується для визначення локальних деформацій в кристалах. Найближчими аналогами запропонованого способу визначення локальних деформацій кристалів на основі профілів розподілу інтенсивності дифрагованих електронів є описані в роботах [2-4] способи аналізу профілів смуг Кікучі. В даних способах-аналогах величина локальної деформації кристалічної ґратки ε=Δdhkl/dhkl (відносна зміна міжплощинної відстані dhkl) пов'язана зі значенням площі під профілем смуги Кікучі за формулою: ε=β·ln(A0/A) (1), де А0 - площа під профілем смуги Кікучі в області кристалу без деформації, А - в -3 деформованій області, коефіцієнт β=4,33·10 [2-4]. Перший недолік описаних способів-аналогів полягає в тому, що обчислення просторового розподілу деформацій кристалу передбачає перетворення до одного масштабу всіх профілів смуг Кікучі, отриманих в локальних областях кристалу. При цьому похибки, що виникають при масштабуванні профілів, зменшують точність обчислення деформацій. Другий недолік способіваналогів полягає в тому, що точність визначення просторового розподілу деформацій кристалів обмежується роздільною здатністю профілю смуги Кікучі, а застосовані методи підвищення роздільної здатності профілю методом інтерполяції з використанням кускових поліноміальних функцій (сплайнів), зокрема лінійних або квадратичних, дають значну похибку [5-7]. Технічною задачею корисної моделі є підвищення точності визначення деформацій в локальних областях кристалу на основі експериментальних профілів розподілу інтенсивності дифрагованих електронів, для чого розроблено новий спосіб обробки профілів смуг Кікучі, отриманих в одному масштабі від локальних областей кристалу. Обробка профілів полягає в їх інтерполяції з адаптивним згладжуванням, при цьому розроблений спосіб забезпечує усунення некоректних осциляцій між вузлами інтерполяції навіть при низьких відношеннях сигнал/шум для значень сигналу в базових точках. Поставлена задача в способі визначення локальних деформацій в множині областей кристалу на основі експериментальних профілів розподілу інтенсивності зворотно відбитих електронів у методі Кікучі вирішується тим, що для кожної області кристалу значення локальної деформації обчислюють через площу під інтерпольованим профілем z(х) смуги Кікучі, отриманої в скануючому електронному мікроскопі від відповідної області досліджуваного кристалу, а значення профілю z(x) отримують шляхом інтерполяції експериментального профілю h(х), заданого в Q базових точках з координатами (хр, hp), де хр - відстань від початку профілю до точки з номером р - 1,…, Q, при цьому для всіх областей кристалу встановлюють однакову відстань від досліджуваної області до СCD детектора скануючого електронного мікроскопа, що забезпечує отримання профілів смуг Кікучі в одному масштабі, а значення інтерпольованого профілю z(х) обчислюють в Qz точках з координатами (xk, zk), де k=1,…, Qz, як суму згладженої функції g (х), яка апроксимує базові точки, та лінійної узгоджуючої функції u(х,р), яка плавно наближує значення функції z(х) до hp у вузлах інтерполяції p, де як функцію g(x) використовують згладжуючі сплайни (Smoothing Spline) з адаптивним згладжуванням. Технічний результат досягається за рахунок того, що за рахунок отримання профілів смуг Кікучі в одному масштабі та їх інтерполяції з адаптивним згладжуванням підвищується точність обчислення площі під інтерпольованим профілем z(x) смуги Кікучі, а відповідно зростає точність визначення деформацій в локальних областях кристалу. Пропонований спосіб визначення локальних деформацій в множині областей кристалу на основі експериментальних профілів Кікучі полягає в тому, що експериментальні профілі h(x) смуг Кікучі отримують в одному масштабі, на основі профілів h(х) обчислюють інтерпольовані 1 UA 100924 U 5 10 15 20 25 30 профілі z(x) зі збільшеною роздільною здатністю, а через площу під профілями z(x) розраховують деформації в локальних областях кристалу. Отримання профілів смуг Кікучі в одному масштабі забезпечується тим, що переміщенням кристалу встановлюють для всіх областей однакову відстань від центру досліджуваної області кристалу до центру CCD детектора скануючого електронного мікроскопа. Інтерпольовані профілі z(x) обчислюють як суму двох складових: 1) згладженої функції g(х), яка апроксимує експериментальні профілі h(x); 2) узгоджуючої функції u(х,р), яка плавно наближує значення функції z(x) до hp у вузлах інтерполяції p, тобто z(x)=g(x)+u(x, p), (2) де р - номер вузла інтерполяції, для якого координата х належить півінтервалу [хр, хр+1). Запропонований спосіб визначення локальних деформацій кристалів використовують у двох режимах: 1. В робочому режимі, який призначений для отримання деформацій кристалів з максимальною точністю, значення експериментального профілю h(x) отримуються на основі картини Кікучі (цифрового зображення) для максимальної кількості базових точок профілю Q. В такому випадку інтерпольований профіль z(х) має збільшену роздільну здатність (Qz>Q), що підвищує точність обчислення площі під профілем смуги Кікучі. 2. В тестовому режимі, який використовується для перевірки точності запропонованого способу, значення експериментального профілю h(x) отримуються на основі картини Кікучі для зменшеної кількості базових точок профілю Q. При цьому з картини Кікучі зчитуються також значення еталонного профілю е(х) в максимальній кількості точок Qe. В такому випадку інтерпольований профіль z(х) має таку ж роздільну здатність, що й еталонний, тобто Qz=Qe. Перевірку точності інтерполяції виконують шляхом порівняння функції z(х) з еталонним профілем e(х). Для кількісної оцінки похибки інтерполяції використовують середню квадратичну різницю Rq між значеннями сигналів z(х) та e(х). При інтерполяції профілів смуг Кікучі як згладжену функцію g(х) використано згладжуючі сплайни (Smoothing Spline), які будуються функцією "csaps" системи Matlab [6]. Ця функція має вигляд: csaps (x, h, S, хх, w), де х і h - вектори координат базових точок хр та hp, де р=1,…, Q, для експериментального профілю h(x), S- параметр згладжування (0≤S≤1), хх - контрольні точки (параметр не обов'язковий), w - вектор ваг (за замовчуванням заповнений одиницями); розрахований згладжений сплайн мінімізує вираз: Q S   hp  zx p   1  S   p 1 35 40 45 50 55 2 ''  z x  dx , (3) xQ 2 x1 При S=0 як згладжену функцію g{x) отримується лінійна функція, а при S=1 - функція, близька до кубічного сплайну. Зміною згладжуючого коефіцієнта S (0≤S≤1) можна коректувати частотну фільтрацію між вузлами інтерполяції: при S=0 пропускаються тільки низькі частоти, при 5=0.5 - низькі і середні, при S=1 всі частоти від низьких до високих. Вибором параметра S можна добитися того, що в результаті інтерполяції будуть пропущені тільки корисні частоти. В той же час використовувати функцію g (х) замість z (x) недопустимо, оскільки в загальному випадку g (x) не проходить через базові точки інтерполяції. Як узгоджуючу функцію u(х,р) для вузлів інтерполяції р та (р+1) на півінтервалі [хр, хр+1) використано лінійні функції, які приймають максимальне значення у вузлі і мінімальні значення у сусідніх вузлах  x  x1   x   hp1  gx p1    1 ux,p   gx   hp  gx p    m  x  x    m m де x m  x p1  x p - відстань між вузлами інтерполяції p   , (4)   та p  1 , x1  x  x p - відстань від поточної координати х до вузла p . Таке представлення функції інтерполяції z(x) забезпечує усунення некоректних осциляцій між вузлами інтерполяції за рахунок адаптивного згладжування, оскільки вибором параметра S для згладженої функції g(x) виконується частотна фільтрації функції z(x), в результаті чого регулюється пропускання частот корисного сигналу і ослаблення складових сигналу з частотами шуму. Оцінку точності запропонованого способу продемонструємо в тестовому режимі на прикладі обробки експериментальних профілів смуг Кікучі, отриманих для локальних областей синтезованого кристалу алмазу за допомогою скануючого растрового електронного мікроскопа [3, 4]. Інтерполяція профілів виконана на основі Q базових точок в системі Matlab. 2 UA 100924 U 5 10 15 20 25 30 35 40 45 50 55 60 Фіг. 1 - катодолюмінісцентне зображення фрагменту поверхні (280×180 мкм) синтезованого кристалу алмазу; маркерами показано області № 1 - № 17, в яких отримані картини Кікучі. Фіг. 2 - картина Кікучі для області № 1 (фіг. 1) синтезованого кристалу алмазу, яку отримано за допомогою скануючого растрового електронного мікроскопа фірми "Zeiss EVO 50" з використанням CCD - детектора; маркерами "+" показано вузли V1-V8 перетину ліній Кікучі та кристалографічні індекси осей зон; початок експериментального профілю h(х) показано чорним кругом; профіль h(х), визначений в Q - 18 т очках, отримано перпендикулярно до смуги Кікучі між вузлами VI та V4 з кристалографічними індексами осей зон [0-11] і [0-13] відповідно; початок і кінець еталонного профілю e(х) такі ж, як для h(x), але значення профілю e(х) визначені в максимальній кількості точок Qe=98; для інших областей кристалу профілі отримуються аналогічно. Фіг. 3 - приклад лінійної інтерполяції (метод "linear") профілю h(x) смуги Кікучі, Rq=0.89418; e - еталонний профіль e(х) (фіг. 2); h - експериментальний профіль h(х); z - результат інтерполяції z(х); в результаті інтерполяції піки і впадини сигналу некоректно обмежуються (обрізаються), наприклад, в областях 1 та 2. Фіг. 4 - приклад інтерполяції кубічними сплайнами (метод "spline") профілю h(x) смуги Кікучі, Rq=0.90887; e - еталонний профіль e(х) (фіг. 2); h - експериментальний профіль h(х); z результат інтерполяції z(x); між вузлами інтерполяції виникають некоректні осциляції, наприклад, в областях 3 та 4. Фіг. 5 - приклад інтерполяції сплайнами Ерміта (Hermite) (метод "cubic") профілю h(x) смуги Кікучі, Rq=0.88221; e - еталонний профіль e(х) (фіг. 2); h - експериментальний профіль h(x); z результат інтерполяції z(x); в результаті інтерполяції піки і впадини сигналу некоректно обмежуються (обрізаються), наприклад, в областях 1 та 2. Фіг. 6 - приклад апроксимації профілю h(x) смуги Кікучі способом згладжуючих сплайнів, обчислення виконані в системі Matlab з використанням функції "csaps", Rq=0.77700; e еталонний профіль e(х) (фіг. 2); h - експериментальний профіль h(х); z - результат інтерполяції z(x), який відрізняється від e(х) менше, ніж результати вищеописаних способів інтерполяції. Фіг. 7 - запропонований спосіб інтерполяції профілю h(x) смуги Кікучі з адаптивним згладжуванням, Rq=0.76657; e - еталонний профіль e(х) (фіг. 2); h - експериментальний профіль h(x); z - результат інтерполяції z(x), який максимально наближений до e(х). Фіг. 8 - середня квадратична різниця Rq для різних методів апроксимації профілю h(x) (фіг. 3 - фіг. 7): SS - спосіб згладжуючих сплайнів (Smoothing Spline), SI - запропонований спосіб інтерполяції одновимірних сигналів з адаптивним згладжуванням (Smoothing Interpolation), в якому за рахунок підбору згладжуючого параметра S досягається найменша середня квадратична різниця Rq порівняно з іншими способами: Linear, Spline, Cubic та згладжуючими сплайнами SS. Фіг. 9 - схема запропонованого алгоритму інтерполяції профілю смуги Кікучі з адаптивним згладжуванням на відрізку [хmin,хmax] з кроком Δх, інтерполяція виконується на основі Q базових точок з координатами (хр, hp), де номер точки p=1,…, Q; оптимальне згладжування результату інтерполяції z(х), який обчислюється як сума функцій g(х) та u(х,р), встановлюється коефіцієнтом S. Фіг. 10 - результат розрахунку деформацій  кристалу в локальних областях (фіг. 1), обчислених через площі під інтерпольованими профілями z(х) смуг Кікучі (фіг. 7) за формулою (1); як область без деформацій вибрано область № 8 за даними методу катодолюмінісценції (фіг. 1); отриманий результат узгоджується з результатом способів-аналогів [2-4], але має вищу точність, оскільки згідно з формулою (1) точність розрахунку деформації  кристалу пропорційна до точності розрахунку площі А під профілем z(х) смуги Кікучі, точність розрахунку площі А визначається похибкою інтерполяції профілю z(х), а в пропонованому способі похибка обчислення z(х) мінімальна (фіг. 8). Таким чином, в порівнянні з способами-аналогами, запропонований спосіб визначення просторового розподілу деформацій досліджуваних кристалів дозволяє точніше визначати деформації в локальних областях за рахунок отримання профілів смуг Кікучі в одному масштабі та їх подальшій інтерполяції з адаптивним згладжуванням. Джерела інформації: 1. Ishido Т. Depth profiles of strain in AlGaN/GaN heterostructures grown on Si characterized by electron backscatter diffraction technique /T. Ishido, H. Matsuo, T. Katayama, T. Ueda, K. Inoue, D. Ueda // IEICE Electronics Express. - 2007. - V. 4, No. 24. - P. 779-783. 2. Sasaki Y. Measuring strains for hematite phase in sinter ore by electron backscattering diffraction method /Y. Sasaki, M. Igushi, M. Hino //Key Engineering materials. - 2006. - V. 326-328. P. 237-240. 3 UA 100924 U 5 10 3. Борча М.Д. Определение структурной неоднородности кристаллов по данным анализа картин Кикучи /М.Д. Борча, С.В. Баловсяк, И.М. Фодчук, В.Ю. Хоменко, В.Н. Ткач //Металлофизика и новейшие технологии. - 2013. - Т. 35, № 8. - С. 1137-1150. 4. Borcha M.D. Distribution of local deformations in diamond crystals according to the analysis of Kikuchi lines profile intensities /M.D. Borcha, S.V. Balovsyak, I.M. Fodchuk, V. Yu. Khomenko, V.N. Tkach //Journal of Superhard Materials. - 2013. - V. 35, No. 4. - P. 220-226. 5. Сизиков В.С. Устойчивые методы обработки результатов измерений /В.С. Сизиков. СПб.: СпецЛит, 1999. - 240 с. 6. Кетков Ю.Л. Matlab 7: программирование, численные методы /Ю.Л. Кетков, А.Ю. Кетков, М.М. Шульц. - СПб.: БХВ-Петербург, 2005. - 752 с. 7. United States Patent № 6,823,234 B2. Toshiaki Otsuki, Hideo Ogino, Soichiro Ide, Takuji Chiba. Curve interpolation method. Nov. 23, 2004. ФОРМУЛА КОРИСНОЇ МОДЕЛІ 15 20 25 Спосіб визначення локальних деформацій кристалів на основі профілів розподілу інтенсивності зворотно відбитих електронів, що отримані за методом Кікучі в множині областей кристалу, який полягає в тому, що для кожної області кристалу значення локальної деформації обчислюють через площу під інтерпольованим профілем z(х) смуги Кікучі, отриманої в скануючому електронному мікроскопі від відповідної області досліджуваного кристалу, а значення профілю z(х) отримують шляхом інтерполяції експериментального профілю h(х), заданого в Q базових точках з координатами (хр, hp), де номер точки р=1,…, Q, який відрізняється тим, що для всіх областей кристалу встановлюють однакову відстань від досліджуваної області на кристалі до CCD детектора скануючого електронного мікроскопа, а значення інтерпольованого профілю z(x) обчислюють як суму згладженої функції g(x), яка апроксимує базові точки, та лінійної узгоджуючої функції u(х,р), яка плавно наближує значення функції z(x) до hp у вузлах інтерполяції р, де як функцію g(x) використовують згладжуючі сплайни (Smoothing Spline) з адаптивним згладжуванням. 4 UA 100924 U 5 UA 100924 U 6 UA 100924 U 7 UA 100924 U 8 UA 100924 U 9 UA 100924 U Комп’ютерна верстка А. Крулевський Державна служба інтелектуальної власності України, вул. Василя Липківського, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут інтелектуальної власності”, вул. Глазунова, 1, м. Київ – 42, 01601 10